题目内容
【题目】(2016年苏州B19)已知函数f(x)=x|x-a|,a∈R,g(x)=x2-1.
(1)当a=1时,解不等式f(x)≥g(x);
(2)记函数f(x)在区间[0,2]上的最大值为F(a),求F(a)的表达式.
【答案】(1)![]() (2)
(2)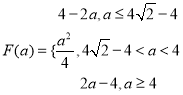
【解析】
【试题分析】(1)借助绝对值的定义讨论当x≥1和x<1两种情形下两个不等式的解集,最后求这两个二次不等式的并集;(2)依据题设条件运用分类整合思想,对实数a≤0;0<a<2;a≥2分三种情形,分别求出函数f(x)在区间[0,2]上的解析式,进而求出其最大值F(a),然后再运用分段函数表示函数F(a)的解析式:
(1)解:f(x)≥g(x),a=1时,即解不等式x|x-1|≥x2-1,
当x≥1时,不等式为x2-x≥x2-1,解得x≤1,所以x=1;
当x<1时,不等式为x-x2≥x2-1,解得![]() ,
,
所以![]() ; 综上, x∈
; 综上, x∈![]() .
.
(2)因为x∈[0,2],当a≤0时,f(x)=x2-ax,则f(x)在区间[0,2]上是增函数,
所以F(a)=f(2)=4-2a;
当0<a<2时,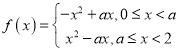 ,则f(x)在区间
,则f(x)在区间![]() 上是增函数,在区间
上是增函数,在区间![]() 上是减函数,在区间[a,2]上是增函数,所以F(a)=max{f(
上是减函数,在区间[a,2]上是增函数,所以F(a)=max{f(![]() ),f(2)},
),f(2)},
而![]() ,f(2)=4-2a,令
,f(2)=4-2a,令![]() 即
即![]() ,
,
解得![]() ,
,
所以当![]() 时,F(a)= 4-2a;
时,F(a)= 4-2a;
令![]() 即
即![]() ,解得
,解得![]() 或
或![]() ,
,
所以当![]() 时,
时,![]() ;
;
当a≥2时,f(x)=-x2+ax,
当![]() 即2≤a<4时,f(x)在间
即2≤a<4时,f(x)在间![]() 上是增函数,在
上是增函数,在![]() 上是减函数,则
上是减函数,则![]() ;
;
当![]() ,即a≥4时,f(x)在间[0,2]上是增函数,则
,即a≥4时,f(x)在间[0,2]上是增函数,则![]() ;
;
所以,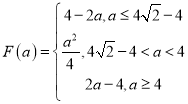 ,
,

【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月对甲、乙两种移动支付方式的使用情况,从全校学生中随机抽取了100人作为样本,发现样本中甲、乙两种支付方式都不使用的有10人,样本中仅使用甲种支付方式和仅使用乙种支付方式的学生的支付金额分布情况如下:
支付金额(元) 支付方式 |
|
| 大于1000 |
仅使用甲 | 15人 | 8人 | 2人 |
仅使用乙 | 10人 | 9人 | 1人 |
(1)从全校学生中随机抽取1人,估计该学生上个月甲、乙两种支付方式都使用的概率;
(2)从样本中仅使用甲种支付方式和仅使用乙种支付方式的学生中各随机抽取1人,以![]() 表示这2人中上个月支付金额大于500元的人数,用频率近似代替概率,求
表示这2人中上个月支付金额大于500元的人数,用频率近似代替概率,求![]() 的分布列和数学期望
的分布列和数学期望

