题目内容
【题目】一古寺有一池储满了水,现一小和尚每日,按照池中所剩水一定的百分率打走一些水,且每次打水的百分率一样.10日过去,池中水恰为满池水的一半.
(1)求此百分率.(保留指数形式)
(2)若某日小和尚打完水,池中水为满池水的![]() 倍,小和尚已打水几日?
倍,小和尚已打水几日?
(3)若某日小和尚打完水,池中水为满池水的![]() 倍,若古寺要求池中水不少于满池水的
倍,若古寺要求池中水不少于满池水的![]() ,则小和尚还能再打几日水?
,则小和尚还能再打几日水?
【答案】(1)
(2)![]()
(3)15
【解析】
(1)设池中满水时为![]() ,设百分比为
,设百分比为![]() ,由题意可得
,由题意可得![]() ,解出
,解出![]() 即可;
即可;
(2)设经过![]() 日还剩为原来的
日还剩为原来的![]() ,可得
,可得![]() ,由(1)将
,由(1)将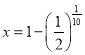 代入求解即可;
代入求解即可;
(3)设还能再打![]() 日,由题意可得
日,由题意可得![]() ,将
,将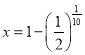 代入求解即可
代入求解即可
设池中满水时为![]() ,
,
(1)设百分比为![]() ,则有:
,则有:
![]() ,即
,即![]() ,所以
,所以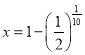
(2)设经过![]() 日还剩为原来的
日还剩为原来的![]() ,则
,则
![]() ,即
,即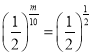 ,所以
,所以![]() ,解得
,解得![]()
(3)设还能再打![]() 日,则
日,则![]() ,即
,即![]() ,
,
所以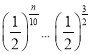 ,即
,即![]() ,解得
,解得![]()
故小和尚还能再打15日

【题目】为弘扬中华传统文化,学校课外阅读兴趣小组进行每日一小时的“经典名著”和“古诗词”的阅读活动. 根据调查,小明同学阅读两类读物的阅读量统计如下:
小明阅读“经典名著”的阅读量![]() (单位:字)与时间t(单位:分钟)满足二次函数关系,部分数据如下表所示;
(单位:字)与时间t(单位:分钟)满足二次函数关系,部分数据如下表所示;
t | 0 | 10 | 20 | 30 |
| 0 | 2700 | 5200 | 7500 |
阅读“古诗词”的阅读量![]() (单位:字)与时间t(单位:分钟)满足如图1所示的关系.
(单位:字)与时间t(单位:分钟)满足如图1所示的关系.

(1)请分别写出函数![]() 和
和![]() 的解析式;
的解析式;
(2)在每天的一小时课外阅读活动中,小明如何分配“经典名著”和“古诗词”的阅读时间,使每天的阅读量最大,最大值是多少?
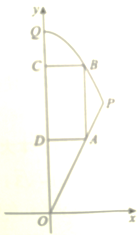
【题目】如图,曲边三角形中,线段![]() 是直线
是直线![]() 的一部分,曲线段
的一部分,曲线段![]() 是抛物线
是抛物线![]() 的一部分.矩形
的一部分.矩形![]() 的顶点分别在线段
的顶点分别在线段![]() ,曲线段
,曲线段![]() 和
和![]() 轴上.设点
轴上.设点![]() ,记矩形
,记矩形![]() 的面积为
的面积为![]() .
.
(Ⅰ)求函数![]() 的解析式并指明定义域;
的解析式并指明定义域;
(Ⅱ)求函数![]() 的最大值.
的最大值.
【答案】(Ⅰ) 定义域为![]() ;(Ⅱ) 在
;(Ⅱ) 在![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
【解析】试题分析:( I )根据点![]() 在直线
在直线![]() 上,
上,![]() 在抛物线
在抛物线![]() 上,结合图形,可得点
上,结合图形,可得点![]() ,从而可得函数
,从而可得函数![]() 的解析式,联立直线与抛物线的方程,即可求得定义域;(II)对函数
的解析式,联立直线与抛物线的方程,即可求得定义域;(II)对函数![]() 求导,利用导数研究函数的单调性,从而可求得函数
求导,利用导数研究函数的单调性,从而可求得函数![]() 的最大值.
的最大值.
试题解析:( I )令![]() ,
,
解得![]()
![]() (舍)
(舍)
因为点![]()
所以![]()
![]() ,
,
其定义域为![]()
(II)因为![]()
令![]() ,得
,得![]() ,
,![]() (舍)
(舍)
所以![]() 的变化情况如下表
的变化情况如下表
|
|
|
|
|
| 0 |
|
|
| 极大 |
|
因为![]() 是函数
是函数![]() 在
在![]() 上的唯一的一个极大值,
上的唯一的一个极大值,
所以在![]() 时,函数
时,函数![]() 取得最大值
取得最大值![]() .
.
点睛:利用导数解答函数最值的一般步骤:第一步:利用![]() 或
或![]() 求单调区间;第二步:解
求单调区间;第二步:解![]() 得两个根
得两个根![]() ;第三步:比较两根同区间端点的大小;第四步:求极值;第五步:比较极值同端点值的大小.
;第三步:比较两根同区间端点的大小;第四步:求极值;第五步:比较极值同端点值的大小.
【题型】解答题
【结束】
16
【题目】在各项均为正数的数列![]() 中,
中,![]()
![]() 且
且![]() .
.
(Ⅰ)当![]() 时,求
时,求![]() 的值;
的值;
(Ⅱ)求证:当![]() 时,
时,![]() .
.
