Question

【题目】数列{an}的通项公式an=ncos ，其前n项和为Sn ， 则S2015=（ ）
A.1008
B.2015
C.﹣1008
D.﹣504

Answer 1

【答案】C
【解析】解：∵an=ncos ， 又∵f（n）=cos 是以T=4为周期的周期函数，
∴a1+a2+a3+a4=（0﹣2+0+4）=2，a5+a6+a7+a8=（0﹣6+0+8）=2，
…
a2009+a2010+a2011+a2012=（0﹣2010+0+2012）=2，
a2013+a2014+a2015=﹣2014．
S2015=a1+a2+a3+a4+…+a2015
=（0﹣2+0+4）+（0﹣6+0+8）+…+（0﹣2010+0+2012）﹣2014
=2×503﹣2014=1006﹣2014=﹣1008．
故选：C．
【考点精析】关于本题考查的数列的前n项和，需要了解数列{an}的前n项和sn与通项an的关系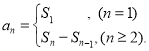才能得出正确答案．