题目内容
8. 图是偶函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,0<φ<π)的部分图象,△KML为等腰直角三角形,∠KML=90°,|KL|=1,则$f(\frac{1}{6})$=( )
图是偶函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,0<φ<π)的部分图象,△KML为等腰直角三角形,∠KML=90°,|KL|=1,则$f(\frac{1}{6})$=( )| A. | -$\frac{{\sqrt{3}}}{4}$ | B. | -$\frac{1}{4}$ | C. | -$\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
分析 通过函数的图象,利用KL以及∠KML=90°求出求出A,然后函数的周期,确定ω,利用函数是偶函数求出φ,即可求解f($\frac{1}{6}$)的值.
解答 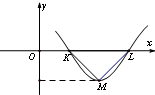 解:因为f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,|KL|=1,
解:因为f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,△KLM为等腰直角三角形,∠KML=90°,|KL|=1,
所以A=$\frac{1}{2}$,T=2,因为T=$\frac{2π}{ω}$,所以ω=π,
函数是偶函数,0<φ<π,所以φ=$\frac{π}{2}$,
∴函数的解析式为:f(x)=$\frac{1}{2}$sin(πx+$\frac{π}{2}$),
所以f($\frac{1}{6}$)=$\frac{1}{2}$sin($\frac{π}{6}$+$\frac{π}{2}$)=$\frac{\sqrt{3}}{4}$.
故选:D.
点评 本题考查函数的解析式的求法,函数奇偶性的应用,考查学生识图能力、计算能力,属于中档题.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
19.直线经过A(2,1),B(1,m2)两点(m∈R),那么直线l的倾斜角的取值范围是( )
| A. | [0,π) | B. | [0,$\frac{π}{4}$]∪($\frac{π}{2}$,π) | C. | [0,$\frac{π}{4}$] | D. | [$\frac{π}{4}$,$\frac{π}{2}$)∪($\frac{π}{2}$,π) |
16.已知$|{\overrightarrow a}|=3$,$|{\overrightarrow b}|=4$,且$\overrightarrow a$与$\overrightarrow b$不共线,若$\overrightarrow a+k\overrightarrow b$与$\overrightarrow a-k\overrightarrow b$垂直时,k的值为( )
| A. | -$\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | ±$\frac{3}{4}$ | D. | ±1 |
3.设集合A={x|y=lg(3-2x)},集合B={y|y=$\sqrt{1-x}$},则A∩B=( )
| A. | [0,$\frac{3}{2}$) | B. | (-∞,1] | C. | (-∞,$\frac{3}{2}$] | D. | ($\frac{3}{2}$,+∞) |
13.已知a为如图所示的算法框图中输出的结果,则二项式${(x+\frac{a}{x^2})^9}$的展开式中的常数项为( )

| A. | 84 | B. | -84 | C. | 672 | D. | -672 |
18.如图所示的是一串黑白相间排列的珠子,若按这种规律排列下去,那么第34颗珠子的颜色是( )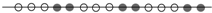
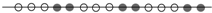
| A. | 白色 | B. | 白色的可能性大 | C. | 黑色 | D. | 黑色的可能性大 |