题目内容
18．已知等比数列{an}中，a1+a3=10，a4+a6=10，求其第4项及前5项的和．分析 设公比为q，运用等比数列的通项公式，列方程，解方程即可得到首项和公比，再由通项公式可得a4的值及前5项的和．
解答 解：设公比为q，
∵a1+a3=10，a4+a6=10，
∴a1+a1q2=10 ①，a1q3+a1q5=10，②
②÷①得q3=1，即有q=1，
将q=1代入①得 a1=5，
则an=a1=5
则a4=a1=5；
S5=5a1=5×5=25．
点评 本题考查等比数列的通项公式和求和公式的运用，考查运算能力，本题求出公比q=1，则数列为常数列．属于基础题．
练习册系列答案
相关题目
8．z=$\frac{{{{（{-1+\sqrt{3}i}）}^3}}}{2^3}+\frac{{-1+\sqrt{2}i}}{{\sqrt{2}+i}}$，则|z|=（ ）
| A． | 2 | B． | $\sqrt{2}$ | C． | $\sqrt{5}$ | D． | 1 |
6．函数f（x）=cos4x，x∈R是（ ）
| A． | 最小正周期是π的偶函数 | B． | 最小正周期是π的奇函数 | ||
| C． | 最小正周期是$\frac{π}{2}$的偶函数 | D． | 最小正周期是$\frac{π}{2}$的奇函数 |
13．函数y=3sin（2x+$\frac{π}{3}$）的图象可以看作是把函数y=3sin2x的图象作下列移动而得到（ ）
| A． | 向左平移$\frac{π}{3}$单位 | B． | 向右平移$\frac{π}{3}$单位 | C． | 向左平移$\frac{π}{6}$单位 | D． | 向右平移$\frac{π}{6}$单位 |
8．
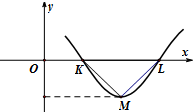图是偶函数f（x）=Asin（ωx+ϕ）（A＞0，ω＞0，0＜φ＜π）的部分图象，△KML为等腰直角三角形，∠KML=90°，|KL|=1，则$f（\frac{1}{6}）$=（ ）
图是偶函数f（x）=Asin（ωx+ϕ）（A＞0，ω＞0，0＜φ＜π）的部分图象，△KML为等腰直角三角形，∠KML=90°，|KL|=1，则$f（\frac{1}{6}）$=（ ）| A． | -$\frac{{\sqrt{3}}}{4}$ | B． | -$\frac{1}{4}$ | C． | -$\frac{1}{2}$ | D． | $\frac{{\sqrt{3}}}{4}$ |