题目内容
已知数列{log2(an-1)}(n∈N*)为等差数列,且a1=3,a3=9.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)证明
+
+…+
<1.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)证明
| 1 |
| a2-a1 |
| 1 |
| a3-a2 |
| 1 |
| an+1-an |
(I)设等差数列{log2(an-1)}的公差为d.
由a1=3,a3=9得2(log22+d)=log22+log28,即d=1.
所以log2(an-1)=1+(n-1)×1=n,即an=2n+1.
(II)证明:因为
=
=
,
所以
+
+…+
=
+
+
+…+
=
=1-
<1,
即得证.
由a1=3,a3=9得2(log22+d)=log22+log28,即d=1.
所以log2(an-1)=1+(n-1)×1=n,即an=2n+1.
(II)证明:因为
| 1 |
| an+1-an |
| 1 |
| 2n+1-2n |
| 1 |
| 2n |
所以
| 1 |
| a2-a1 |
| 1 |
| a3-a2 |
| 1 |
| an+1-an |
| 1 |
| 21 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| ||||||
1-
|
| 1 |
| 2n |
即得证.

练习册系列答案
相关题目
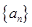 中,若
中,若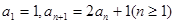
 ,设
,设 ,
, 是等比数列;
是等比数列;
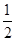
 中,
中, =( )
=( )