题目内容
在△ABC中,a、b、c分别为∠A、∠B、∠C的对边,若a、b、c成等差数列,sinB=
且△ABC的面积为
,求b.
| 4 |
| 5 |
| 3 |
| 2 |
∵由a、b、c成等差数列,得a+c=2b
∴平方得a2+c2=4b2-2ac------①…(2分)
又∵S△ABC=
且sinB=
,
∴S△ABC=
ac•sinB=
ac×
=
ac=
故ac=
-------②…(4分)
由①②联解,可得a2+c2=4b2-
-------③…(5分)
又∵sinB=
,且a、b、c成等差数列
∴cosB=
=
=
.…(8分)
由余弦定理得:
b2=a2+c2-2ac•cosB=a2+c2-2×
×
=a2+c2-
-------④…(10分)
由③④联解,可得b2=4,所以b=2.…(12分)
∴平方得a2+c2=4b2-2ac------①…(2分)
又∵S△ABC=
| 3 |
| 2 |
| 4 |
| 5 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 5 |
| 2 |
| 5 |
| 3 |
| 2 |
故ac=
| 15 |
| 4 |
由①②联解,可得a2+c2=4b2-
| 15 |
| 2 |
又∵sinB=
| 4 |
| 5 |
∴cosB=
| 1-sin2B |
1-
|
| 3 |
| 5 |
由余弦定理得:
b2=a2+c2-2ac•cosB=a2+c2-2×
| 15 |
| 4 |
| 3 |
| 5 |
| 9 |
| 2 |
由③④联解,可得b2=4,所以b=2.…(12分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是等比数列,满足
是等比数列,满足 ,且
,且 ,
, ,则
,则 ( )
( )



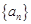 的各项都是正数,且
的各项都是正数,且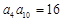 ,则
,则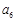 =( )
=( )