题目内容
已知点A（-2，-3）、B（3，2），若直线l：y=kx+1与线段AB有公共点，则斜率k的取值范围是
(-∞，
]∪[2，+∞)
| 1 |
| 3 |
(-∞，
]∪[2，+∞)
．| 1 |
| 3 |
分析：意直线l：y=kx+1过定点（0，1），作出图象，求出边界直线的斜率，且直线由m开始，逆时针旋转时斜率增大，进而可得要求的范围．
解答：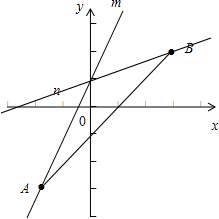
解：由题意可得直线l：y=kx+1过定点（0，1），如图
当直线介于m，n之间时，满足题意，
km=
=2，kn=
=
，
且直线由m开始，逆时针旋转时斜率增大，
故斜率的取值范围为：(-∞，
]∪[2，+∞)
故答案为：(-∞，
]∪[2，+∞)
解：由题意可得直线l：y=kx+1过定点（0，1），如图当直线介于m，n之间时，满足题意，
km=
| 1-(-3) |
| 0-(-2) |
| 1-2 |
| 0-3 |
| 1 |
| 3 |
且直线由m开始，逆时针旋转时斜率增大，
故斜率的取值范围为：(-∞，
| 1 |
| 3 |
故答案为：(-∞，
| 1 |
| 3 |
点评：本题考查直线的斜率，数形结合是解决问题的关键，属基础题．
练习册系列答案
相关题目
