题目内容
(本题满分18分,其中第1小题6分,第2小题4分,第3小题8分)
定义变换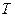 :
: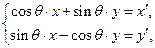 可把平面直角坐标系上的点
可把平面直角坐标系上的点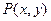 变换到这一平面上的点
变换到这一平面上的点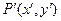 .特别地,若曲线
.特别地,若曲线 上一点
上一点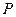 经变换公式
经变换公式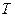 变换后得到的点
变换后得到的点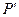 与点
与点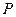 重合,则称点
重合,则称点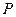 是曲线
是曲线 在变换
在变换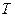 下的不动点.
下的不动点.
(1)若椭圆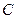 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在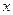 轴上,且焦距为
轴上,且焦距为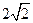 ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆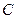 的标准方程. 并求出当
的标准方程. 并求出当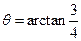 时,其两个焦点
时,其两个焦点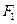 、
、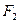 经变换公式
经变换公式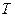 变换后得到的点
变换后得到的点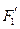 和
和 的坐标;
的坐标;
(2)当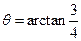 时,求(1)中的椭圆
时,求(1)中的椭圆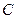 在变换
在变换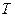 下的所有不动点的坐标;
下的所有不动点的坐标;
(3)试探究:中心为坐标原点、对称轴为坐标轴的双曲线在变换
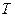 :
: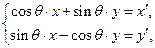 (
(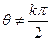 ,
,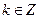 )下的不动点的存在情况和个数.
)下的不动点的存在情况和个数.
定义变换
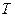 :
: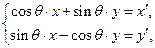 可把平面直角坐标系上的点
可把平面直角坐标系上的点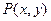 变换到这一平面上的点
变换到这一平面上的点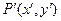 .特别地,若曲线
.特别地,若曲线 上一点
上一点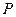 经变换公式
经变换公式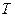 变换后得到的点
变换后得到的点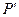 与点
与点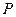 重合,则称点
重合,则称点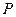 是曲线
是曲线 在变换
在变换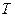 下的不动点.
下的不动点.(1)若椭圆
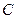 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在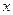 轴上,且焦距为
轴上,且焦距为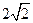 ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆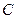 的标准方程. 并求出当
的标准方程. 并求出当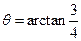 时,其两个焦点
时,其两个焦点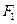 、
、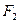 经变换公式
经变换公式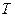 变换后得到的点
变换后得到的点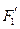 和
和 的坐标;
的坐标;(2)当
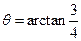 时,求(1)中的椭圆
时,求(1)中的椭圆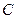 在变换
在变换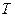 下的所有不动点的坐标;
下的所有不动点的坐标;(3)试探究:中心为坐标原点、对称轴为坐标轴的双曲线在变换
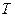 :
: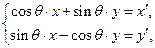 (
(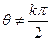 ,
,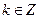 )下的不动点的存在情况和个数.
)下的不动点的存在情况和个数.(1)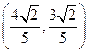 (2)
(2)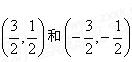 (3)两个
(3)两个
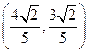 (2)
(2)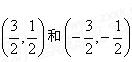 (3)两个
(3)两个(1)设椭圆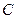 的标准方程为 的标准方程为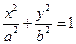 ( (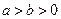 ),由椭圆定义知焦距 ),由椭圆定义知焦距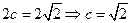 ,即 ,即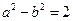 …①. …①.又由条件得 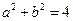 …②,故由①、②可解得 …②,故由①、②可解得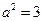 , ,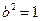 . .即椭圆  的标准方程为 的标准方程为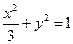 . . 且椭圆  两个焦点的坐标分别为 两个焦点的坐标分别为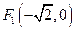 和 和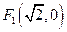 . .对于变换 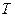 : :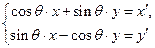 ,当 ,当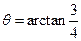 时,可得 时,可得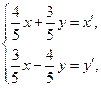 设 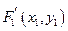 和 和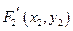 分别是由 分别是由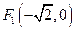 和 和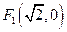 的坐标由变换公式 的坐标由变换公式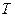 变换得到.于是, 变换得到.于是,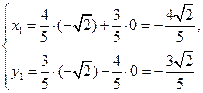 ,即 ,即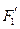 的坐标为 的坐标为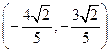 ; ;又 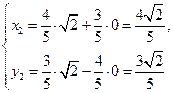 即 即 的坐标为 的坐标为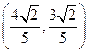 . .(2)设 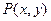 是椭圆 是椭圆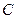 在变换 在变换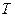 下的不动点,则当 下的不动点,则当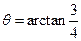 时, 时,有 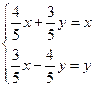 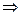 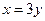 ,由点 ,由点 ,即 ,即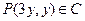 ,得: ,得: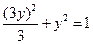 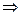 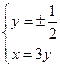 , , 因而椭圆 因而椭圆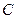 的不动点共有两个,分别为 的不动点共有两个,分别为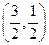 和 和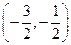 . .(3) 设 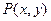 是双曲线在变换 是双曲线在变换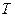 下的不动点,则由 下的不动点,则由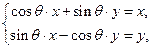 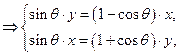 因为 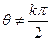 , ,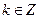 ,故 ,故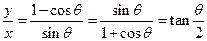 . .不妨设双曲线方程为 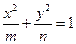 ( (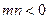 ),由 ),由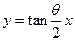 代入得 代入得则有 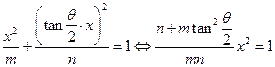 , ,因为 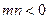 ,故当 ,故当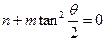 时,方程 时,方程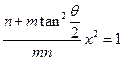 无解; 无解;当 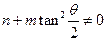 时,要使不动点存在,则需 时,要使不动点存在,则需 , ,因为 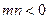 ,故当 ,故当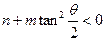 时,双曲线 时,双曲线 在变换 在变换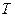 下一定有2个不动点,否则不存 下一定有2个不动点,否则不存 在不动点. 在不动点.进一步分类可知: (i)当 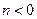 , ,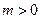 时,即双曲线的焦点在 时,即双曲线的焦点在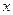 轴上时, 轴上时,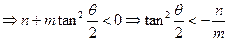 ; ;此时双曲线在变换 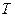 下一定有2个不动点; 下一定有2个不动点;(ii)当 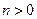 , ,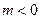 时,即双曲线的焦点在 时,即双曲线的焦点在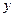 轴上时, 轴上时,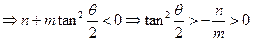 . . |
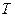 下一定有2个不动点.
下一定有2个不动点.
练习册系列答案
相关题目
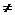 b)和点N(x0,y0),则称直线l:ax0x+by0y=1为椭圆C的“伴随直线”,
b)和点N(x0,y0),则称直线l:ax0x+by0y=1为椭圆C的“伴随直线”,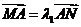 ,
,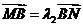 ,问
,问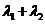 是否为定值?说明理由.
是否为定值?说明理由. 轴上的椭圆C的离心率为
轴上的椭圆C的离心率为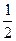 ,且经过点
,且经过点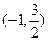 ,过点P(2,1)的直线
,过点P(2,1)的直线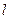 与椭圆C在第一象限相切于点M .
与椭圆C在第一象限相切于点M . 与椭圆C相交于不同的两点A、B,满足
与椭圆C相交于不同的两点A、B,满足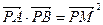 ?若存在,求出直线l1的方程;若不存在,请说明理由.
?若存在,求出直线l1的方程;若不存在,请说明理由.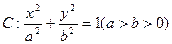 的左、右焦点分别为F1与F2,直线
的左、右焦点分别为F1与F2,直线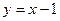 过椭圆的一个焦点F2且与椭圆交于P、Q两点,若
过椭圆的一个焦点F2且与椭圆交于P、Q两点,若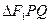 的周长为
的周长为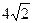 。
。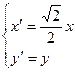 变成曲线
变成曲线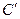 ,直线
,直线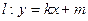 与曲线
与曲线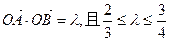 ,求
,求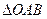 面积的取值范围。(O为坐标原点)
面积的取值范围。(O为坐标原点)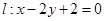 与坐标轴的交点分别是一个椭圆的焦点和顶点,则此椭圆的离心率为 ( )
与坐标轴的交点分别是一个椭圆的焦点和顶点,则此椭圆的离心率为 ( )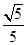
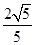
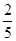
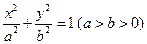 的左焦点
的左焦点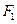 作x轴的垂线交椭圆于点P,点A和点B分别为椭圆的右顶点和上顶点,OP∥AB.
作x轴的垂线交椭圆于点P,点A和点B分别为椭圆的右顶点和上顶点,OP∥AB.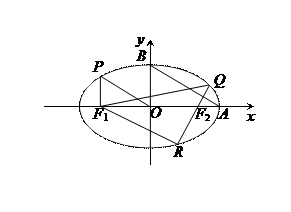 (2)过右焦点
(2)过右焦点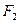 作一条弦QR,使QR⊥AB.若△
作一条弦QR,使QR⊥AB.若△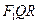 的面积为
的面积为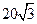 ,求椭圆的方程.
,求椭圆的方程.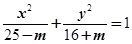 表示焦点在y轴上的椭圆,则m的取值范围为 .
表示焦点在y轴上的椭圆,则m的取值范围为 .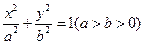 的右焦点且垂直于
的右焦点且垂直于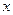 轴的直线与椭圆交于
轴的直线与椭圆交于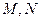 两点,以
两点,以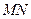 为直径的圆恰好过左焦点,则椭圆的离心率等于 。
为直径的圆恰好过左焦点,则椭圆的离心率等于 。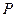 是以
是以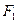 ,
, 为焦点的椭圆
为焦点的椭圆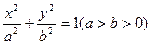 上的一点,若
上的一点,若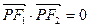 ,
,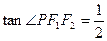 ,则此椭圆的离心率为____________.
,则此椭圆的离心率为____________.