题目内容
设函数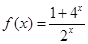
(1)判断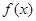 的奇偶性
的奇偶性
(2)用定义法证明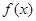 在
在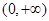 上单调递增
上单调递增
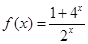
(1)判断
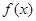 的奇偶性
的奇偶性(2)用定义法证明
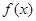 在
在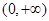 上单调递增
上单调递增(1)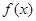 为偶函数。
为偶函数。
(2)设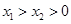 ,则
,则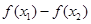
 ,由于
,由于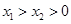 ,得
,得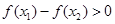 ,所以
,所以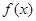 在
在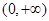 上单调递增
上单调递增
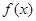 为偶函数。
为偶函数。(2)设
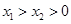 ,则
,则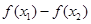
 ,由于
,由于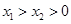 ,得
,得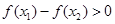 ,所以
,所以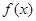 在
在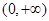 上单调递增
上单调递增试题分析:(1)函数
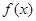 的定义域为
的定义域为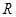 ,关于原点对称。
,关于原点对称。 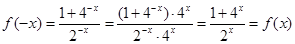 ,所以
,所以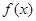 为偶函数。
为偶函数。(2)设
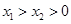 ,则
,则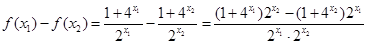
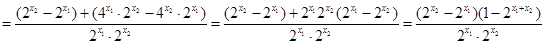
由于
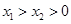 ,所以
,所以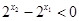 ;
;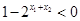 ,
,所以
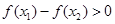
所以
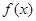 在
在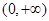 上单调递增
上单调递增点评:典型题,研究函数的奇偶性,首先定义域应关于原点对称,其次研究
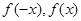 的关系。利用定义证明函数的单调性,遵循“设,作差,定号,结论”等步骤。
的关系。利用定义证明函数的单调性,遵循“设,作差,定号,结论”等步骤。
练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
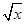 )2
)2
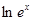 与g(x)=
与g(x)=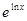
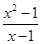 与g(t)=t+1(t≠1)
与g(t)=t+1(t≠1)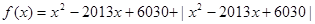 ,则
,则
 _ .
_ .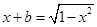 有实数解,则实数b的范围是_______________
有实数解,则实数b的范围是_______________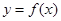 在区间
在区间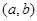 上的导函数为
上的导函数为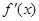 ,
,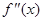 ,若在区间
,若在区间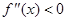 恒成立,则称函数
恒成立,则称函数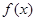 在区间
在区间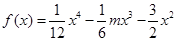 ,若对任意的实数
,若对任意的实数 满足
满足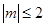 时,函数
时,函数 的最大值为
的最大值为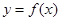 的图象与直线
的图象与直线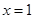 的公共点数目是( )
的公共点数目是( )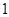

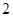

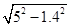 -0.8=4,
-0.8=4,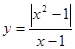 的图象与函数
的图象与函数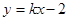 的图象恰有两个交点,则实数k的取值范围是_________.
的图象恰有两个交点,则实数k的取值范围是_________.