题目内容
已知△ABC中, 点A,B的坐标分别为A(- ,0),B(
,0),B( ,0)点C在x轴上方.
,0)点C在x轴上方.
(Ⅰ)若点C坐标为( ,1),求以A,B为焦点且经过点C的椭圆的方程:
,1),求以A,B为焦点且经过点C的椭圆的方程:
(Ⅱ)过点P(m,0)作倾斜角为 的直线l交(1)中曲线于M,N两点,若点Q(1,0)恰在以线段MN为直径的圆上,求实数m的值.
的直线l交(1)中曲线于M,N两点,若点Q(1,0)恰在以线段MN为直径的圆上,求实数m的值.
(Ⅰ)椭圆方程为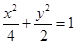 ;(Ⅱ)
;(Ⅱ)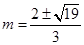 .
.
解析试题分析:(Ⅰ)由椭圆定义易求;(Ⅱ)此题是直线与椭圆位置关系的问题,可采用设而不求的解题方法,设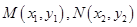 ,由已知可得直线
,由已知可得直线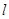 的方程为
的方程为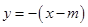 ,代入椭圆方程,得到关于
,代入椭圆方程,得到关于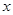 的一元二次方程,注意到点P(m,0)不一定在椭圆内部,需对方程是否有解讨论, 点
的一元二次方程,注意到点P(m,0)不一定在椭圆内部,需对方程是否有解讨论, 点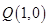 恰在以线段
恰在以线段 为直径的圆上,说明
为直径的圆上,说明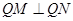 ,它们的斜率互为负倒数,利用根与系数关系,建立方程,从而求出实数m的值.此题易错点,不知对方程是否有解讨论.
,它们的斜率互为负倒数,利用根与系数关系,建立方程,从而求出实数m的值.此题易错点,不知对方程是否有解讨论.
试题解析:(Ⅰ)设椭圆方程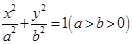 ,
,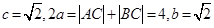 ,
,
椭圆方程为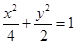 ;
;
(Ⅱ)直线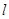 的方程为
的方程为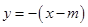 ,令
,令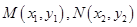 ,联立方程得:
,联立方程得: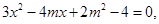
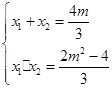 ,
,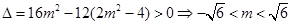 ,
,
若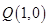 恰在以线段
恰在以线段 为直径的圆上,则
为直径的圆上,则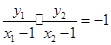 ,即
,即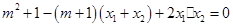 ,
, 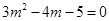 ,解得
,解得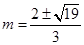 ,
,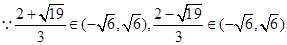 ,
,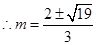 符合题意
符合题意
考点:椭圆的方程,直线与椭圆的位置关系,考查学生的运算能力、化简能力以及数形结合的能力.

练习册系列答案
相关题目
 +
+ =1(a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°
=1(a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°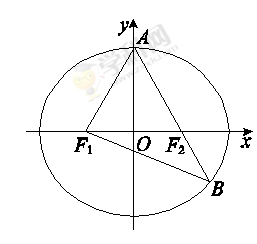
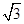 ,求a,b的值
,求a,b的值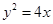 的焦点为F2,点F1与F2关于坐标原点对称,以F1,F2为焦点的椭圆C过点
的焦点为F2,点F1与F2关于坐标原点对称,以F1,F2为焦点的椭圆C过点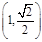 .
.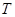
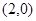 ,过点F2作直线
,过点F2作直线 与椭圆C交于A,B两点,且
与椭圆C交于A,B两点,且 ,若
,若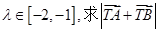 的取值范围.
的取值范围.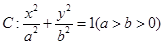 的离心率为
的离心率为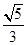 ,定点
,定点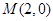 ,椭圆短轴的端点是
,椭圆短轴的端点是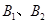 ,且
,且 .
.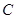 的方程;
的方程; 且斜率不为0的直线交椭圆
且斜率不为0的直线交椭圆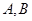 两点.试问
两点.试问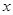 轴上是否存在异于
轴上是否存在异于 ,使
,使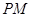 平分
平分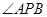 ?若存在,求出点
?若存在,求出点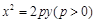 相交于B、C,当直线l的斜率是
相交于B、C,当直线l的斜率是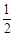 时,
时,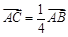 .
.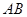 长为2m,跳水板距水面
长为2m,跳水板距水面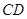 的高
的高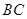 为3m,
为3m, =5m,
=5m,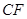 =6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点
=6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点 m(
m(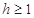 )时达到距水面最大高度4m,规定:以
)时达到距水面最大高度4m,规定:以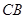 为纵轴建立直角坐标系.
为纵轴建立直角坐标系.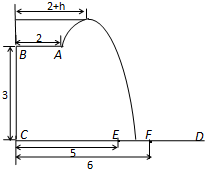
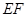 内入水时才能达到压水花的训练要求,求达到压水花的训练要求时
内入水时才能达到压水花的训练要求,求达到压水花的训练要求时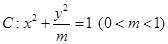 的左顶点为
的左顶点为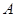 ,
,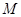 是椭圆
是椭圆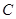 上异于点
上异于点 与点
与点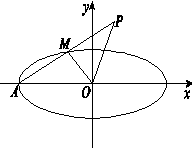
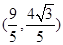 ,求
,求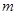 的值;
的值;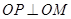 ,求
,求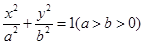 的左焦点为
的左焦点为 ,离心率为
,离心率为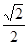 ,过点
,过点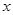 轴垂直的直线被椭圆截得的线段长为
轴垂直的直线被椭圆截得的线段长为 .
.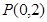 的直线
的直线 与椭圆交于不同的两点
与椭圆交于不同的两点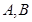 ,当
,当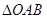 面积最大时,求
面积最大时,求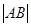 .
.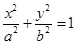 (a>b>0)的两个焦点和短轴的两个端点都在圆
(a>b>0)的两个焦点和短轴的两个端点都在圆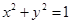 上.
上.