题目内容
【题目】已知：a，b，c∈（﹣∞，0），求证：a+ 
，b+ 
，c+ 
中至少有一个不大于﹣2．
【答案】证明：假设 
中没有一个不大于﹣2
即： 
， 
， 
所以有 
即 
又因为a＜0，b＜0，c＜0，则﹣a＞0，﹣b＞0，﹣c＞0
所以有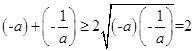 
，（当且仅当 
即a=﹣1时取等号）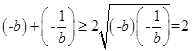
，（当且仅当 
即b=﹣1时取等号）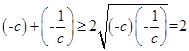
，（当且仅当 
即c=﹣1时取等号）
所以 
， 
， 
所以 
（当且仅当2时取等号）
与 矛盾
所以假设错误，原命题正确．
所以 中至少有一个不大于﹣2
【解析】首先根据题意，通过反证法假设 
中没有一个不大于﹣2，得出 
， 
， 
，即 
，然后根据基本不等式，得出 
，相互矛盾，即可证明．
【考点精析】解答此题的关键在于理解反证法与放缩法的相关知识，掌握常见不等式的放缩方法：①舍去或加上一些项②将分子或分母放大（缩小)．
练习册系列答案
相关题目
