题目内容
已知 和
和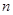 均为给定的大于1的自然数.设集合
均为给定的大于1的自然数.设集合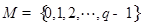 ,集合
,集合 .
.
(1)当 ,
, 时,用列举法表示集合
时,用列举法表示集合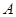 ;
;
(2)设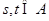 ,
, ,
, ,其中
,其中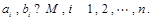 证明:若
证明:若 ,则
,则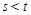 .
.
(1) ;(2)详见试题分析.
;(2)详见试题分析.
解析试题分析:(1)当 时,
时,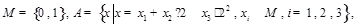 采用列举法可得集合
采用列举法可得集合 ;(2)先由已知写出
;(2)先由已知写出 及
及 的表达式:
的表达式: ,
, ,再作差可得
,再作差可得 ,放缩法化为
,放缩法化为 最后利用等比数列前
最后利用等比数列前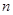 项和公式求和,判断出差式的符号,证得结果.
项和公式求和,判断出差式的符号,证得结果.
(1)当 时,
时,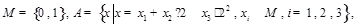 可得,
可得, .
.
(2)由 及
及 ,可得
,可得
 .
.
考点:1.集合的含义与表示;2.等比数列的前 项和公式;3.不等式的证明.
项和公式;3.不等式的证明.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
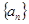 的前n项和为
的前n项和为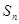
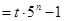 ,则
,则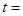
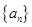 所有项均为正数,首
所有项均为正数,首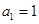 ,且
,且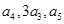 成等差数列.
成等差数列.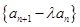 的前n项和为
的前n项和为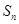 ,若
,若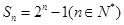 ,求实数
,求实数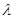 的值.
的值.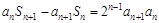 ,
,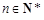 .
.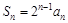 ;
;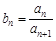 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn. ,
, 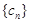 满足条件:
满足条件: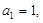
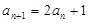 ,
, 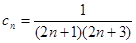 .
.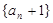 是等比数列,并求数列
是等比数列,并求数列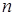 项和
项和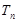 ,并求使得
,并求使得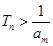 对任意
对任意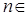 N*都成立的正整数
N*都成立的正整数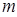 的最小值.
的最小值.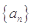 的前
的前 项和为
项和为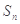 ,且满足
,且满足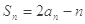 ,
,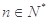
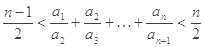
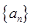 的前
的前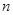 项和为
项和为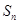 ,且
,且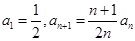 .
.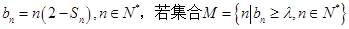 恰有5个元素,求实数
恰有5个元素,求实数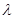 的取值范围.
的取值范围. 的等比数列{an}的前n项和为Sn(n∈N*),且-2S2,S3,4S4成等差数列.
的等比数列{an}的前n项和为Sn(n∈N*),且-2S2,S3,4S4成等差数列.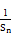 ≤
≤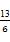 (n∈N*).
(n∈N*).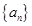 的首项
的首项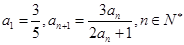 .
.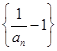 为等比数列;
为等比数列;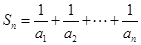 ,若
,若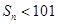 ,求最大正整数
,求最大正整数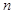 的值;
的值;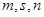 ,使
,使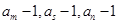 成等比数列?如果存在,请给予证明;如果不存在,请说明理由.
成等比数列?如果存在,请给予证明;如果不存在,请说明理由.