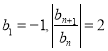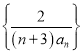题目内容
【题目】已知椭圆![]() 的短轴两端点与左焦点围成的三角形面积为3,短轴两端点与长轴一端点围成的三角形面积为2,设椭圆
的短轴两端点与左焦点围成的三角形面积为3,短轴两端点与长轴一端点围成的三角形面积为2,设椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() 是椭圆
是椭圆![]() 上除
上除![]() 两点外一动点.
两点外一动点.
(1)求椭圆![]() 的方程;
的方程;
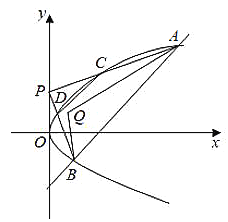
(2)过椭圆![]() 的左焦点作平行于直线
的左焦点作平行于直线![]() (
(![]() 是坐标原点)的直线
是坐标原点)的直线![]() ,
,![]() 与曲线
与曲线![]() 交于
交于![]() 两点,点
两点,点![]() 关于原点
关于原点![]() 的对称点为
的对称点为![]() ,求证:
,求证:![]() 成等比数列.
成等比数列.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)根据题意和椭圆中![]() 的关系,列出方程组,解这个方程组即可;
的关系,列出方程组,解这个方程组即可;
(2)依题意,要证![]() 成等比数列,只需证
成等比数列,只需证![]() ,即
,即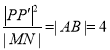 .设出直线
.设出直线![]() 的方程、直线
的方程、直线![]() 的方程,分别与椭圆方程联立,结合根与系数关系,求出相应线段的长度进行证明即可.
的方程,分别与椭圆方程联立,结合根与系数关系,求出相应线段的长度进行证明即可.
(1)解:依题意,得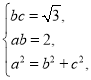 解得
解得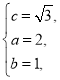 故椭圆
故椭圆![]() 的方程为
的方程为![]() .
.
(2)证明:依题意,要证![]() 成等比数列,
成等比数列,
只需证![]() ,即
,即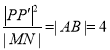 .设直线
.设直线![]() ,直线
,直线![]() ,
,
联立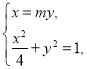 得
得![]() ,
,![]() ,故
,故![]() .
.
联立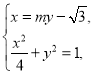 得
得![]() .
.
设![]() ,则
,则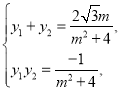
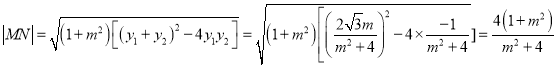 ,
,
∴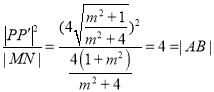 ,所以
,所以![]() 成等比数列.
成等比数列.

练习册系列答案
相关题目
【题目】某保险公司给年龄在![]() 岁的民众提供某种疾病的一年期医疗保险,现从
岁的民众提供某种疾病的一年期医疗保险,现从![]() 名参保人员中随机抽取
名参保人员中随机抽取![]() 名作为样本进行分析,按年龄段
名作为样本进行分析,按年龄段![]() 、
、![]() 、
、![]() 、
、![]() 、
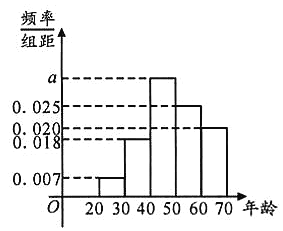
、![]() 分成了五组,其频率分布直方图如下图所示,参保年龄与每人每年应交纳的保费如下表所示.
分成了五组,其频率分布直方图如下图所示,参保年龄与每人每年应交纳的保费如下表所示.
年龄(单位:岁) |
|
|
|
|
|
保费(单位:元) |
|
|
|
|
|
(1)求频率分布直方图中实数![]() 的值,并求出该样本年龄的中位数;
的值,并求出该样本年龄的中位数;
(2)现分别在年龄段![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中各选出
中各选出![]() 人共
人共![]() 人进行回访.若从这
人进行回访.若从这![]() 人中随机选出
人中随机选出![]() 人,求这
人,求这![]() 人所交保费之和大于
人所交保费之和大于![]() 元的概率.
元的概率.