题目内容
【题目】某厂生产![]() 和
和![]() 两种产品,按计划每天生产
两种产品,按计划每天生产![]() 各不得少于10吨,已知生产
各不得少于10吨,已知生产![]() 产品
产品![]() 吨需要用煤9吨,电4度,劳动力3个(按工作日计算).生产
吨需要用煤9吨,电4度,劳动力3个(按工作日计算).生产![]() 产品1吨需要用煤4吨,电5度,劳动力10个,如果
产品1吨需要用煤4吨,电5度,劳动力10个,如果![]() 产品每吨价值7万元,
产品每吨价值7万元, ![]() 产品每吨价值12万元,而且每天用煤不超过300吨,用电不超过200度,劳动力最多只有300个,每天应安排生产
产品每吨价值12万元,而且每天用煤不超过300吨,用电不超过200度,劳动力最多只有300个,每天应安排生产![]() 两种产品各多少才是合理的?
两种产品各多少才是合理的?
【答案】![]() 产品20吨和
产品20吨和![]() 产品
产品![]() 吨是合理的.
吨是合理的.
【解析】试题分析:设每天生产![]() 产品
产品![]() 吨和
吨和![]() 产品
产品![]() 吨,根据用煤量、用电量、劳动力的限制列出关于,
吨,根据用煤量、用电量、劳动力的限制列出关于, ![]() 的约束条件,画出可行域,平移目标函数
的约束条件,画出可行域,平移目标函数![]() ,即可找到最优解,代入目标函数即可得结果.
,即可找到最优解,代入目标函数即可得结果.
试题解析:设每天生产![]() 产品
产品![]() 吨和
吨和![]() 产品
产品![]() 吨,则创造的价值为
吨,则创造的价值为![]() (万元),由已知列出的约束条件为
(万元),由已知列出的约束条件为
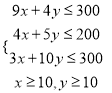 ,问题就成为在此二元一次不等式组限制的范围(区域)内寻找
,问题就成为在此二元一次不等式组限制的范围(区域)内寻找![]() ,使目标函数
,使目标函数![]() 取最大值的问题,画出可行域如图.
取最大值的问题,画出可行域如图.
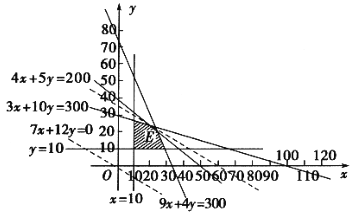
∵![]() ,∴当直线
,∴当直线![]() 经过直线
经过直线![]() 与
与![]() 的交点
的交点![]() 时,
时, ![]() 最大,解方程组
最大,解方程组![]() 得
得![]() ,∴
,∴![]() 点坐标为
点坐标为![]() ,∴当
,∴当![]() 时,
时, ![]() 取最大值.
取最大值.
答:每天生产![]() 产品20吨和
产品20吨和![]() 产品
产品![]() 吨是合理的.
吨是合理的.
【方法点晴】本题主要考查线性规划的应用、利用可行域求目标函数的最值,属中档题.求目标函数最值的一般步骤是“一画、二移、三求”:(1)作出可行域(一定要注意是实线还是虚线);(2)找到目标函数对应的最优解对应点(在可行域内平移变形后的目标函数,最先通过或最后通过的顶点就是最优解);(3)将最优解坐标代入目标函数求出最值.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目