题目内容
4.已知椭圆c1:$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1的左、右焦点分别为F1,F2,过点F1作垂直于x轴的直线l1,直线l2垂直l1于点P,线段PF2的垂直平分线交l2于点M(1)求点M的轨迹C2的方程
(2)过点F2作两条互相垂直的直线AC,BD,且分别交椭圆于A,B,C,D,求四边形ABCD面积的最小值.
分析 (1)求得椭圆的焦点坐标,连接MF2,由垂直平分线的性质可得|MP|=|MF2|,运用抛物线的定义,即可得到所求轨迹方程;
(2)分类讨论:当AC或BD中的一条与x轴垂直而另一条与x轴重合时,此时四边形ABCD面积S=2b2.当直线AC和BD的斜率都存在时,不妨设直线AC的方程为y=k(x-2),则直线BD的方程为y=-$\frac{1}{k}$(x-2).分别与椭圆的方程联立得到根与系数的关系,利用弦长公式可得|AC|,|BD|.利用四边形ABCD面积S═$\frac{1}{2}$|AC|•|BD|即可得到关于斜率k的式子,再利用配方和二次函数的最值求法,即可得出.
解答 解:(1)椭圆c1:$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1的焦点F1(-2,0),F2(2,0),
连接MF2,由垂直平分线的性质可得|MP|=|MF2|,
由抛物线的定义,可得M的轨迹为以F2为焦点,l1为准线的抛物线,
即有方程为y2=8x;
(2)由椭圆$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1可得a2=8,b2=4,c=$\sqrt{{a}^{2}-{b}^{2}}$=2.
①当AC或BD中的一条与x轴垂直而另一条与x轴重合时,
此时四边形ABCD面积S=$\frac{1}{2}$•2a•$\frac{2{b}^{2}}{a}$=2b2=8.
②当直线AC和BD的斜率都存在时,不妨设直线AC的方程为y=k(x-2),
则直线CD的方程为y=-$\frac{1}{k}$(x-2).
联立$\left\{\begin{array}{l}{y=k(x-2)}\\{{x}^{2}+2{y}^{2}=8}\end{array}\right.$,化为(1+2k2)x2-8k2x+8k2-8=0,
∴x1+x2=$\frac{8{k}^{2}}{1+2{k}^{2}}$,x1x2=$\frac{8{k}^{2}-8}{1+2{k}^{2}}$.
∴|AC|=$\sqrt{(1+{k}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=$\sqrt{(1+{k}^{2})[(\frac{8{k}^{2}}{1+2{k}^{2}})^{2}-\frac{32{k}^{2}-32}{1+2{k}^{2}}]}$=$\frac{4\sqrt{2}(1+{k}^{2})}{1+2{k}^{2}}$.
把k换成-$\frac{1}{k}$,可得|BD|=$\frac{4\sqrt{2}(1+{k}^{2})}{2+{k}^{2}}$.
∴四边形ABCD面积S=$\frac{1}{2}$|AC|•|BD|=$\frac{1}{2}$•$\frac{4\sqrt{2}(1+{k}^{2})}{1+2{k}^{2}}$•$\frac{4\sqrt{2}(1+{k}^{2})}{2+{k}^{2}}$
=$\frac{16(1+{k}^{2})^{2}}{2{k}^{4}+5{k}^{2}+2}$=$\frac{16}{-(\frac{1}{1+{k}^{2}}-\frac{1}{2})^{2}+\frac{9}{4}}$,
当且仅当$\frac{1}{1+{k}^{2}}$=$\frac{1}{2}$,即k2=1时,S取得最小值$\frac{16}{\frac{9}{4}}$=$\frac{64}{9}$.
综上可知:四边形ABCD面积S的最小值是$\frac{64}{9}$.
点评 本题考查抛物线的定义和方程,同时考查椭圆的标准方程及其性质、相互垂直的直线斜率之间的关系、直线与椭圆相交问题转化为方程联立得到根与系数的关系、弦长公式、四边形面积计算公式、二次函数的最值求法等基础知识与基本技能方法,考查了推理能力和计算能力,属于中档题.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案| A. | n2 | B. | n2+n | C. | 2n2+3n | D. | n2+$\frac{5}{2}n$ |
| A. | -$\frac{\sqrt{13}}{13}$ | B. | $\frac{\sqrt{13}}{13}$ | C. | -$\frac{2\sqrt{13}}{13}$ | D. | $\frac{2\sqrt{13}}{13}$ |
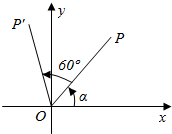 如图,保持点P(3,3)与原点的距离不变,并绕原点旋转60°到P′位置,设点P′的坐标为(x′,y′).
如图,保持点P(3,3)与原点的距离不变,并绕原点旋转60°到P′位置,设点P′的坐标为(x′,y′).