题目内容
.(12分)
如图,△ABC内接于⊙O,过点A的直线交⊙O于点P,交BC的延长线于点D,
且AB2=AP·AD
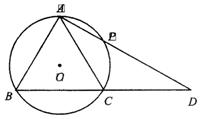
(1)求证:AB=AC;
(2)如果∠ABC=60°,⊙O的半径为1,且P为弧AC的中点,求AD的长.
【答案】
(1)证明:联结BP.
∵AB2=AP·AD,∴ .
.
∵∠BAD=∠PAB,∴△ABD∽△APB,
∴∠ABC=∠APB,∵∠ACB=∠APB,
∴∠ABC=∠ACB.∴AB=AC.
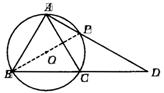
(2)由(1)知AB=AC.∵∠ABC=60°,∴△ABC是等边三角形.
∴∠BAC=60°,∵P为弧AC的中点,
∴∠ABP=∠PAC=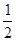 ∠ABC=30°,∴∠BAP=90°,∴ BP是⊙O的直径,∴
BP=2,∴AP=
∠ABC=30°,∴∠BAP=90°,∴ BP是⊙O的直径,∴
BP=2,∴AP=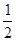 BP=1,
BP=1,
在Rt△PAB中,由勾股定理得 AB=BP2-AP2=3,∴AD=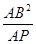 =3.
=3.
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
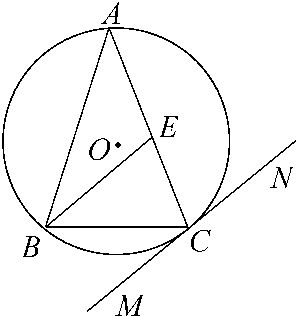 如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E.若AB=6,BC=4,求AE的长.
如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E.若AB=6,BC=4,求AE的长.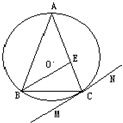 (1)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线
(1)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线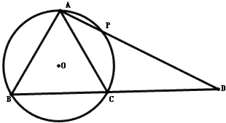 如图,△ABC内接于⊙O,过点A的直线交⊙O于点P,交BC的延长线于点D,且AB2=AP•AD
如图,△ABC内接于⊙O,过点A的直线交⊙O于点P,交BC的延长线于点D,且AB2=AP•AD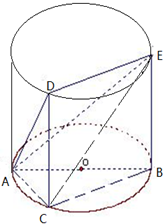 如图,△ABC内接于圆柱的底面圆O,AB是圆O的直径,AB=2,BC=1,DC、EB是两条母线,且 tan∠EAB=
如图,△ABC内接于圆柱的底面圆O,AB是圆O的直径,AB=2,BC=1,DC、EB是两条母线,且 tan∠EAB=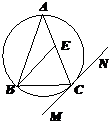 如图:△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E,若AB=6,BC=4,则AE的长为( )
如图:△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E,若AB=6,BC=4,则AE的长为( )