题目内容
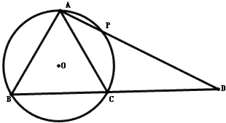 如图,△ABC内接于⊙O,过点A的直线交⊙O于点P,交BC的延长线于点D,且AB2=AP•AD
如图,△ABC内接于⊙O,过点A的直线交⊙O于点P,交BC的延长线于点D,且AB2=AP•AD(Ⅰ)求证:∠ABC=∠ACB
(Ⅱ)如果∠ABC=60°,⊙O的半径为1,且P为弧AC的中点,求AD的长.
分析:(Ⅰ)连接BP,由已知等式变形得到比例式,再由一对公共角相等,得三角形ABD与三角形APB相似,由相似三角形的对应角相等得到一对角相等,再利用圆周角定理得到一对角相等,等量代换即可得证;
(Ⅱ)由第一问的结论得到AB=AC,再由∠ABC=60°,得到三角形ABC为等边三角形,由P为弧AC中点,利用弧,圆心角及弦之间的关系得到BP为角平分线,求出∠ABC=30°,进而确定出三角形ABP为直角三角形,确定出BP为圆的直径,确定出BP的长,再利用30度角所对的直角边等于斜边的一半求出AP的长,李艳艳余弦定理求出AB的长,代入已知等式中计算即可求出AD的长.
(Ⅱ)由第一问的结论得到AB=AC,再由∠ABC=60°,得到三角形ABC为等边三角形,由P为弧AC中点,利用弧,圆心角及弦之间的关系得到BP为角平分线,求出∠ABC=30°,进而确定出三角形ABP为直角三角形,确定出BP为圆的直径,确定出BP的长,再利用30度角所对的直角边等于斜边的一半求出AP的长,李艳艳余弦定理求出AB的长,代入已知等式中计算即可求出AD的长.
解答: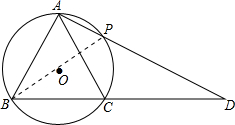 解:(Ⅰ)证明:连接BP,
解:(Ⅰ)证明:连接BP,
∵AB2=AP•AD,∴
=
,
又∵∠BAD=∠PAB,
∴△ABD∽△APB,
∴∠ABC=∠APB,
∵∠ACB=∠APB,
∴∠ABC=∠ACB;
(Ⅱ)由(Ⅰ)知:AB=AC,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴∠ABC=60°,
∵P为弧AC的中点,
∴∠ABP=∠PAC=
∠ABC=30°,
∴∠BAP=90°,
∴BP是圆O的直径,
∴BP=2,
∴AP=
BP=1,
在Rt△PAB中,由勾股定理得:AB=
,
∴AD=
=3.
 解:(Ⅰ)证明:连接BP,
解:(Ⅰ)证明:连接BP,∵AB2=AP•AD,∴
| AB |
| AP |
| AD |
| AB |
又∵∠BAD=∠PAB,
∴△ABD∽△APB,
∴∠ABC=∠APB,
∵∠ACB=∠APB,
∴∠ABC=∠ACB;
(Ⅱ)由(Ⅰ)知:AB=AC,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴∠ABC=60°,
∵P为弧AC的中点,
∴∠ABP=∠PAC=
| 1 |
| 2 |
∴∠BAP=90°,
∴BP是圆O的直径,
∴BP=2,
∴AP=
| 1 |
| 2 |
在Rt△PAB中,由勾股定理得:AB=
| 3 |
∴AD=
| AB2 |
| AP |
点评:此题考查了余弦定理,相似三角形的判定与性质,等边三角形的判定与性质,以及含30度直角三角形的性质,熟练掌握余弦定理是解本题的关键.

练习册系列答案
相关题目
 如图,△ABC内接于圆O,AB是圆O的直径,AB=2,BC=1,设AE与平面ABC所成的角为θ,且tanθ=
如图,△ABC内接于圆O,AB是圆O的直径,AB=2,BC=1,设AE与平面ABC所成的角为θ,且tanθ=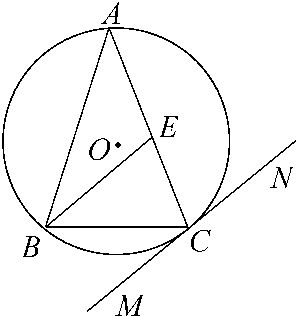 如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E.若AB=6,BC=4,求AE的长.
如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E.若AB=6,BC=4,求AE的长.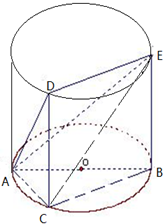 如图,△ABC内接于圆柱的底面圆O,AB是圆O的直径,AB=2,BC=1,DC、EB是两条母线,且 tan∠EAB=
如图,△ABC内接于圆柱的底面圆O,AB是圆O的直径,AB=2,BC=1,DC、EB是两条母线,且 tan∠EAB=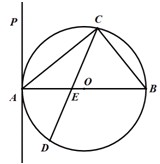 (2013•沈阳二模)选修4-1:几何证明选讲
(2013•沈阳二模)选修4-1:几何证明选讲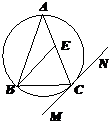 如图:△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E,若AB=6,BC=4,则AE的长为( )
如图:△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E,若AB=6,BC=4,则AE的长为( )