题目内容
 (1)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线ρsin(θ+
(1)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线ρsin(θ+| π |
| 3 |
(2)已知2x+y=1,x>0,y>0,则
| x+2y |
| xy |
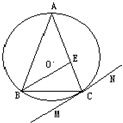
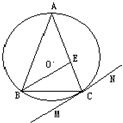
(3)如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E.若AB=6,BC=4,则AE的长为
分析:(1)把极坐标方程化为普通方程,利用点到直线的距离公式求出圆心到直线的距离,最小距离等于圆心到直线的距离减去半径.
(2)由题意得
=
+
=
+
=
+
+5,利用基本不等式求最小值.
(3)由题意得∠BCM=∠CBE=∠BAC,∠BCE=∠ACB,根据△ABC∽△BEC,对应边成比例,求出 CE 的长,即可得到AE的长.
(2)由题意得
| x+2y |
| xy |
| 1 |
| y |
| 2 |
| x |
| 2x+y |
| y |
| 4x+2y |
| x |
| 2x |
| y |
| 2y |
| x |
(3)由题意得∠BCM=∠CBE=∠BAC,∠BCE=∠ACB,根据△ABC∽△BEC,对应边成比例,求出 CE 的长,即可得到AE的长.
解答:解:(1)曲线ρ=2sinθ 即 ρ2=2ρ sinθ,x2+y2=2y,x2+(y-1)2=1,
表示以(0,1)为圆心,以1为半径的圆.
直线ρsin(θ+
)=4 即
ρsinθ+
ρcosθ=4,
x+y-8=0.
圆心到直线的距离等于
=
,故点A到直线ρsin(θ+
)=4的距离的最小值是
-1=
,
故答案为
.
(2)
=
+
=
+
=
+
+5≥2
+5=9,
故
的最小值是 9,故答案为 9.
(3)由题意得∠BCM=∠CBE=∠BAC,∠BCE=∠ACB,∴△ABC∽△BEC,
∴
=
,
=
,∴CE=
,AE=AC-CE=6-
=
,
故答案为
.
表示以(0,1)为圆心,以1为半径的圆.
直线ρsin(θ+
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
圆心到直线的距离等于
| |0+1-8| | ||
|
| 7 |
| 2 |
| π |
| 3 |
| 7 |
| 2 |
| 5 |
| 2 |
故答案为
| 5 |
| 2 |
(2)
| x+2y |
| xy |
| 1 |
| y |
| 2 |
| x |
| 2x+y |
| y |
| 4x+2y |
| x |
| 2x |
| y |
| 2y |
| x |
|
故
| x+2y |
| xy |
(3)由题意得∠BCM=∠CBE=∠BAC,∠BCE=∠ACB,∴△ABC∽△BEC,
∴
| AB |
| BC |
| BC |
| CE |
| 6 |
| 4 |
| 4 |
| CE |
| 8 |
| 3 |
| 8 |
| 3 |
| 10 |
| 3 |
故答案为
| 10 |
| 3 |
点评:本题考查把极坐标方程化为普通方程的方法,点到直线的距离公式的应用,直线和圆的位置关系;基本不等式的应用,利用三角形相似求线段的长度.

练习册系列答案
相关题目
 (1)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线
(1)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线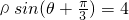 的距离的最小值是________.
的距离的最小值是________.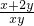 的最小值是________.
的最小值是________.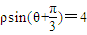 的距离的最小值是 .
的距离的最小值是 .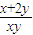 的最小值是 .
的最小值是 .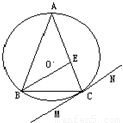
 的距离的最小值是 .
的距离的最小值是 . 的最小值是 .
的最小值是 .