题目内容
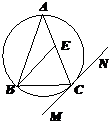 如图:△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E,若AB=6,BC=4,则AE的长为( )
如图:△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E,若AB=6,BC=4,则AE的长为( )分析:根据直线MN切⊙O于点C,由弦线角定理我们易得∠BCM=∠A,再由BE∥MN,我们可得∠BCM=∠EBC,我们可判断出△ABC∽△BEC,由相似三角形对应边成比例,代入AB=6,BC=4,可求出AE的长.
解答:解:直线MN切⊙O于点C,
∵根据弦切角可知∠BCM=∠A,BE∥MN,
∴∠BCM=∠EBC,∠A=∠EBC.又∠ACB是公共角,
∴根据三角对应相等得到△ABC∽△BEC,
∴
=
.
∵AB=AC=6,BC=4,
∴EC=
=
=
,
∴AE=AC-EC=6-
=
.
故选A
∵根据弦切角可知∠BCM=∠A,BE∥MN,
∴∠BCM=∠EBC,∠A=∠EBC.又∠ACB是公共角,
∴根据三角对应相等得到△ABC∽△BEC,
∴
| AC |
| BC |
| BC |
| EC |
∵AB=AC=6,BC=4,
∴EC=
| BC2 |
| AC |
| 42 |
| 6 |
| 8 |
| 3 |
∴AE=AC-EC=6-
| 8 |
| 3 |
| 10 |
| 3 |
故选A
点评:本题考查弦切角定理,考查三角形相似的判定与性质,本题解题的关键是根据已知条件判断出△ABC∽△BEC,进而得到得到三角形对应边成比例,本题是一个中档题目.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
 如图,△ABC内接于圆O,AB是圆O的直径,AB=2,BC=1,设AE与平面ABC所成的角为θ,且tanθ=
如图,△ABC内接于圆O,AB是圆O的直径,AB=2,BC=1,设AE与平面ABC所成的角为θ,且tanθ=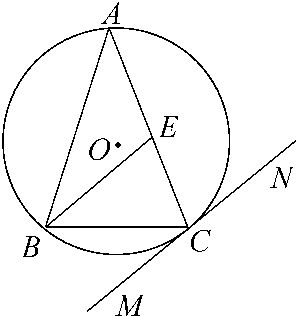 如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E.若AB=6,BC=4,求AE的长.
如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,BE∥MN交AC于点E.若AB=6,BC=4,求AE的长.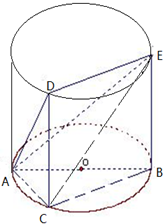 如图,△ABC内接于圆柱的底面圆O,AB是圆O的直径,AB=2,BC=1,DC、EB是两条母线,且 tan∠EAB=
如图,△ABC内接于圆柱的底面圆O,AB是圆O的直径,AB=2,BC=1,DC、EB是两条母线,且 tan∠EAB=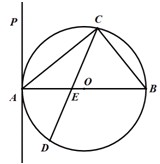 (2013•沈阳二模)选修4-1:几何证明选讲
(2013•沈阳二模)选修4-1:几何证明选讲