题目内容
【题目】某车间共有![]() 名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
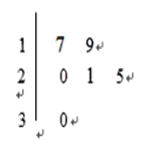
(Ⅰ) 根据茎叶图计算样本均值;
(Ⅱ) 日加工零件个数大于样本均值的工人为优秀工人,根据茎叶图推断该车间![]() 名工人中有几名优秀工人;
名工人中有几名优秀工人;
(Ⅲ) 从该车间![]() 名工人中,任取2人,求恰有1名优秀工人的概率.
名工人中,任取2人,求恰有1名优秀工人的概率.
【答案】(1)22;(2)4;(3)![]() .
.
【解析】试题分析:(1)由茎叶图能求出样本均值;(2)由抽取的6名工人中有2名为优秀工人,得到12名工人中有4名优秀工人;(3)设“从该车间12名工人中,任取2人,恰有1名优秀工人”为事件A,由等可能事件概率计算公式能求出恰有1名优秀工人的概率.
试题解析:(1)由题意可知,样本均值![]() .
.
(2) ![]() 样本6名个人中日加工零件个数大于样本均值的工人共有2名,
样本6名个人中日加工零件个数大于样本均值的工人共有2名, ![]() 可以推断该车间12名工人中优秀工人的人数为:
可以推断该车间12名工人中优秀工人的人数为: ![]() .
.
(3)![]() 从该车间12名工人中,任取2人有
从该车间12名工人中,任取2人有![]() 种方法, 而恰有1名优秀工人有
种方法, 而恰有1名优秀工人有![]() ,故所求的概率为:
,故所求的概率为: ![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目