题目内容
已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1,动点M到圆C的切线长与|MQ|的比等于常数λ(λ>0).求动点M的轨迹方程,说明它表示什么曲线。
当λ=1时,方程化为x= ,它表示一条直线,该直线与x轴垂直且交x轴于点(
,它表示一条直线,该直线与x轴垂直且交x轴于点( ,0);
,0);
当λ≠1时,方程化为 它表示圆,圆心的坐标为(
它表示圆,圆心的坐标为( ),半径为
),半径为 。
。
解析试题分析:
思路分析:利用“直接法”求得(λ2-1)(x2+y2)-4λ2x+(1+4λ2)=0.
讨论λ=1和λ≠1的两种情况。
当λ=1时,方程化为x= ,它表示一条直线,该直线与x轴垂直且交x轴于
,它表示一条直线,该直线与x轴垂直且交x轴于
点( ,0);
,0);
当λ≠1时,方程化为 它表示圆,圆心的坐标为(
它表示圆,圆心的坐标为( ),半径为
),半径为 。
。
解:设MN切圆于N,则动点M组成的集合是P={M||MN|=λ|MQ|},式中常数λ>0.因为圆的半径|ON|=1,
所以|MN|2=|MO|2-|ON|2=|MO|2-1.
设点M的坐标为(x,y),则 ,
,
整理得(λ2-1)(x2+y2)-4λ2x+(1+4λ2)=0.
经检验,坐标适合这个方程的点都属于集合P.故这个方程为所求的轨迹方程.
当λ=1时,方程化为x= ,它表示一条直线,该直线与x轴垂直且交x轴于
,它表示一条直线,该直线与x轴垂直且交x轴于
点( ,0);
,0);
当λ≠1时,方程化为 它表示圆,圆心的坐标为(
它表示圆,圆心的坐标为( ),半径为
),半径为 。
。
考点:求轨迹方程
点评:中档题,求轨迹方程方法较多,本题利用直接法:直接法是将动点满足的几何条件或者等量关系,直接坐标化,列出等式化简即得动点轨迹方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的三个顶点
的三个顶点 ,
, ,
, ,其外接圆为
,其外接圆为 .
. 过点
过点 ,且被
,且被 上的任意一点
上的任意一点 ,若在以
,若在以 ,使得点
,使得点 是线段
是线段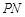 的中点,求
的中点,求 的半径
的半径 的取值范围.
的取值范围.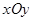 中,点
中,点 ,直线
,直线 。设圆
。设圆 的半径为
的半径为 ,圆心在
,圆心在 上。
上。
 上,过点
上,过点 作圆
作圆 ,使
,使 ,求圆心
,求圆心 的取值范围。.
的取值范围。. (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点. 关于直线
关于直线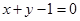 对称,圆心
对称,圆心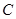 在第二象限,半径为
在第二象限,半径为 .
. 与圆
与圆 轴、
轴、 轴上的截距相等?若存在,求直线的方程;若不存在,说明理由。
轴上的截距相等?若存在,求直线的方程;若不存在,说明理由。 ,直线
,直线 经过点
经过点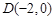 ,
, ,
, 两点,且
两点,且 为等腰直角三角形,求直线
为等腰直角三角形,求直线 的方程.
的方程.  与圆
与圆 相交,求实数m的取值范围;
相交,求实数m的取值范围; 被直线
被直线 截得的弦长.
截得的弦长. :
: ,圆
,圆 方程为
方程为
 的值
的值