题目内容
【题目】已知函数f(x)=x2﹣2|x|﹣1.
(1)证明函数f(x)是偶函数;
(2)在如图所示的平面直角坐标系中作出函数f(x)的图象.并根据图象写出函数f(x)的单调区间; 
(3)求函数f(x)当x∈[﹣2,4]时的最大值与最小值.
【答案】
(1)证明:∵x∈R,f(﹣x)=(﹣x)2﹣2|﹣x|﹣1=x2﹣2|x|+1=f(x),
∴f(x)是偶函数
(2)解:∵当x≥0时,f(x)=x2﹣2x﹣1,当x<0时,f(x)=x2+2x﹣1,
则函数f(x)图象如图所示
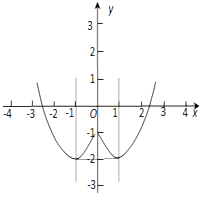
(3)解:由图知当x=﹣1和1时有最小值为﹣2.当x=4时有最大值7
【解析】(1)根据偶函数的定义即可证明,(2)去绝对值,化为分段函数,画图即可,(3)由图象可求出f(x)当x∈[﹣2,4]时的最大值与最小值.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减才能正确解答此题.
上递减才能正确解答此题.

练习册系列答案
相关题目

