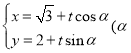题目内容
【题目】已知2件次品和3件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束.
(1)求第一次检测出的是次品且第二次检测出的是正品的概率;
(2)已知每检测一件产品需要费用100元,设X表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求![]() .
.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)根据古典概型公式得到第一次检测出次品的概率,第二次检测出正品的概率,由分步计数原理得到答案;(2)根据题意,进行了![]() 次检测,测出2件次品或者检测出3件正品,分类进行研究,然后利用分类计数原理,得到答案.
次检测,测出2件次品或者检测出3件正品,分类进行研究,然后利用分类计数原理,得到答案.
解: (1)第一次检测出的是次品且第二次检测出的是正品的概率为
![]() .
.
(2)由题意可知![]() ,表示一共进行了
,表示一共进行了![]() 次检测,
次检测,
![]() 次检测都是正品,概率为
次检测都是正品,概率为![]() ,
,
进行![]() 次检测,有
次检测,有![]() 件次品,
件次品,![]() 件正品,
件正品,
所以前两次检测是![]() 件正品和
件正品和![]() 件次品,第三次检测是次品,
件次品,第三次检测是次品,
概率为![]()
![]() ,
,
所以![]() .
.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
【题目】根据调查,某学校开设了“街舞”、“围棋”、“武术”三个社团,三个社团参加的人数如下表所示:
社团 | 街舞 | 围棋 | 武术 |
人数 | 320 | 240 | 200 |
为调查社团开展情况,学校社团管理部采用分层抽样的方法从中抽取一个容量为n的样本,已知从“围棋”社团抽取的同学比从“街舞”社团抽取的同学少2人.
(1)求三个社团分别抽取了多少同学;
(2)若从“围棋”社团抽取的同学中选出2人担任该社团活动监督的职务,已知“围棋”社团被抽取的同学中有2名女生,求至少有1名女同学被选为监督职务的概率。