题目内容
已知f(x)=(1+mx)2013=a+a1x+a2x2+…+a2013x2013(x∈R)(1)若m=
 ,求m、a及a1的值;
,求m、a及a1的值;(2)若离散型随机变量X~B(4,
 )且m=EX时,令bn=(-1)nnan,求数列{bn}的前2013项的和T2013.
)且m=EX时,令bn=(-1)nnan,求数列{bn}的前2013项的和T2013.
【答案】分析:(1)求出原函数,即可求得积分,利用赋值法,可求a及a1的值;
(2)利用二项分布的期望公式,可求m的值,利用函数关系式,两边求导,再赋值,即可得到结论.
解答:解:(1)∵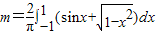
∴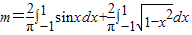 =
=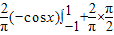 =1,
=1,
则: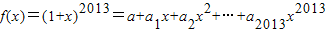 ,
,
令x=0得:a=1,且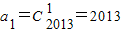 ;
;
(2)∵离散型随机变量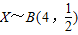 且m=EX
且m=EX
∴m=2,
∴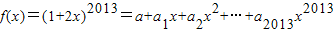
则两边取导得: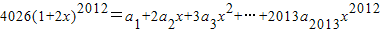
令x=-1得:4026(1-2)2012=a1-2a2+3a3-4a4…+2013a2013
即:-a1+2a2-3a3+4a4-…-2013a2013=-4026;
∴数列{bn}的前2013项的和T2013=-4026.
点评:本题考查定积分,考查二项式定理的运用,考查学生的计算能力,属于中档题.
(2)利用二项分布的期望公式,可求m的值,利用函数关系式,两边求导,再赋值,即可得到结论.
解答:解:(1)∵
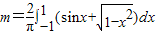
∴
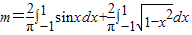 =
=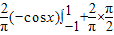 =1,
=1,则:
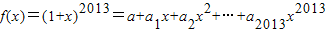 ,
,令x=0得:a=1,且
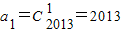 ;
;(2)∵离散型随机变量
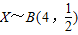 且m=EX
且m=EX∴m=2,
∴
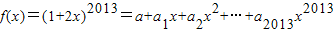
则两边取导得:
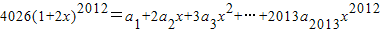
令x=-1得:4026(1-2)2012=a1-2a2+3a3-4a4…+2013a2013
即:-a1+2a2-3a3+4a4-…-2013a2013=-4026;
∴数列{bn}的前2013项的和T2013=-4026.
点评:本题考查定积分,考查二项式定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
已知f(x)=a-
是定义在R上的奇函数,则f-1(-
)的值是( )
| 2 |
| 2x+1 |
| 3 |
| 5 |
A、
| ||
| B、-2 | ||
C、
| ||
D、
|