题目内容
7.已知m>n>0,a,b∈R+且(a-1)(b-1)≠0,求证:(an+bn)m>(am+bm)n.分析 先运用分析法:要证(an+bn)m>(am+bm)n.即证mln(an+bn)>nln(am+bm),(m>n>0)即证$\frac{ln({a}^{n}+{b}^{n})}{n}$>$\frac{ln({a}^{m}+{b}^{m})}{m}$,可设f(x)=$\frac{ln({a}^{x}+{b}^{x})}{x}$(x>0,a,b∈R+且a,b≠1),求出导数,判断单调性,即可得证.
解答 证明:要证(an+bn)m>(am+bm)n.
即证mln(an+bn)>nln(am+bm),(m>n>0)
即证$\frac{ln({a}^{n}+{b}^{n})}{n}$>$\frac{ln({a}^{m}+{b}^{m})}{m}$,
可设f(x)=$\frac{ln({a}^{x}+{b}^{x})}{x}$(x>0,a,b∈R+且a,b≠1),
则f′(x)=$\frac{\frac{x}{{a}^{x}+{b}^{x}}•({a}^{x}lna+{b}^{x}lnb)-ln({a}^{x}+{b}^{x})}{{x}^{2}}$,
由x•axlna+x•bxlnb-axln(ax+bx)-bxln(ax+bx)
=axln$\frac{{a}^{x}}{{a}^{x}+{b}^{x}}$+bxln$\frac{{b}^{x}}{{a}^{x}+{b}^{x}}$
由0<$\frac{{a}^{x}}{{a}^{x}+{b}^{x}}$<1,ln$\frac{{a}^{x}}{{a}^{x}+{b}^{x}}$<0,
由0<$\frac{{b}^{x}}{{a}^{x}+{b}^{x}}$<1,ln$\frac{{b}^{x}}{{a}^{x}+{b}^{x}}$<0,
即有x•axlna+x•bxlnb-axln(ax+bx)-bxln(ax+bx)<0,
即f′(x)<0,f(x)在(0,+∞)递减,
当m>n时,$\frac{ln({a}^{n}+{b}^{n})}{n}$>$\frac{ln({a}^{m}+{b}^{m})}{m}$,
故原不等式成立.
点评 本题考查不等式的证明,注意运用分析法和构造函数,由导数判断单调性,考查推理能力,属于中档题.

| A. | $\frac{16}{3}$ | B. | 32 | C. | $\frac{64\sqrt{3}}{9}$ | D. | $\frac{128\sqrt{3}}{3}$ |
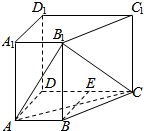 如图,在四棱锥ABCD-A1B1C1D中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0),现将与四棱锥ABCD-A1B1C1D形状和大小完全相同的两个四棱柱拼接成一个新的棱柱,规定:若拼接成的新的四棱锥形状和大小完全相同,则视为同一种拼接方案.问:共有几种不同的方案?在这些拼接成的新的四棱柱中,记其中最小的表面积为f(k),写出f(k)的表达式.
如图,在四棱锥ABCD-A1B1C1D中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0),现将与四棱锥ABCD-A1B1C1D形状和大小完全相同的两个四棱柱拼接成一个新的棱柱,规定:若拼接成的新的四棱锥形状和大小完全相同,则视为同一种拼接方案.问:共有几种不同的方案?在这些拼接成的新的四棱柱中,记其中最小的表面积为f(k),写出f(k)的表达式.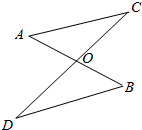 如图,线段AB、CD交于点O,且$\frac{AO}{OB}$=$\frac{CO}{OD}$,用向量的运算证明AC∥DB.
如图,线段AB、CD交于点O,且$\frac{AO}{OB}$=$\frac{CO}{OD}$,用向量的运算证明AC∥DB.