题目内容
8.已知函数f(x)=log(2a-1)(2x+1)在区间(0,+∞)上满足f(x)>0,则a的取值范围是(1,+∞).分析 利用对数函数的图象与性质即可得出答案.
解答 解:∵x∈(0,+∞),∴2x+1∈(1,+∞);
又∵f(x)>0,
∴2a-1>1,
解得a>1,
∴a的取值范围是(1,+∞).
点评 本题考查了对数函数的图象与性质的应用问题,是基础题目.

练习册系列答案
相关题目
17.设函数f(x)=logax,若不等式|f(x)|>1对任意x∈[2,+∞)恒成立,则实数a的取值范围是( )
| A. | (0,$\frac{1}{2}$)∪(1,2) | B. | (0,$\frac{1}{2}$)∪(2,+∞) | C. | ($\frac{1}{2}$,1)∪(1,2) | D. | ($\frac{1}{2}$,1)∪(2,+∞) |
18.若sin($\frac{π}{2}$+θ)<0,且cos($\frac{π}{2}-θ$)>0,则θ是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
15.若执行如图的程序框图,则输出的n的值是( )


| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
13.在△ABC中,角A、B、C的对边分别是a、b、c,其中b=c=2,若函数f(x)=$\frac{1}{4}{x^3}-\frac{3}{4}x$的极大值是cosA,则△ABC的面积等于( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
17.若复数z=$\frac{a-i}{1-i}$(a∈R,i是虚数单位)是纯虚数,则复数3-z的共轭复数是( )
| A. | 3+i | B. | 3-i | C. | 3+2i | D. | 2-i |
18.下列函数中,与函数y=x表示同一函数的是( )
| A. | $f(x)=\sqrt{x^2}$ | B. | $f(x)=\root{5}{x^5}$ | C. | $f(x)={(\sqrt{x})^2}$ | D. | f(x)=|x| |
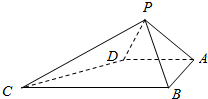 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形.
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形.