题目内容
9.某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是138cm2
分析 根据几何体的三视图得到几何体的结构,进行求解即可.
解答 解:由三视图可知该几何体是个组合体,右侧是一个棱长分别为3,4,6的长方体,
左侧是个平放的三棱柱,三棱柱的高为3,底面直角三角形的两个直角边为3和4,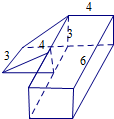
则长方体的表面积为2×(3×4+3×6+4×6)-3×3=108-9=99,
三棱柱的表面积为3×5+3×4+2×$\frac{1}{2}×4×3$=39,
则几何体的表面积为99+39=138,(cm2)
故答案为:138.
点评 本题主要考查空间组合体的表面积的计算,根据条件左侧空间几何体的直观图是解决本题的关键.

练习册系列答案
相关题目
13.已知$\overrightarrow{AB}$=$\overrightarrow a+5\overrightarrow b$,$\overrightarrow{BC}$=$-2\overrightarrow a+8\overrightarrow b$,$\overrightarrow{CD}=3({\overrightarrow a-\overrightarrow b})$,且$\overrightarrow a,\overrightarrow b$不共线,则( )
| A. | A.B.D三点共线 | B. | A.B.C三点共线 | C. | B.C.D三点共线 | D. | A.C.D三点共线 |
4.棱长为2的正四面体ABCD在空间直角坐标系中移动,但保持点A、B分别在x轴、y轴上移动,则棱CD的中点E到坐标原点O的最远距离为( )
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$+1 | D. | $\sqrt{2}$+1 |
1.参数方程为$\left\{\begin{array}{l}{x=t+\frac{1}{t}}\\{y=2}\end{array}\right.$(t为参数)表示的曲线是( )
| A. | 两条射线 | B. | 两条直线 | C. | 一条射线 | D. | 一条直线 |
19.已知函数f(x)=ax,则“0<a≤$\frac{1}{4}$”是“对任意x1≠x2,都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<0成立”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
 已知二次函数f(x)=ax2+bx+2的导函数的图象如图所示:
已知二次函数f(x)=ax2+bx+2的导函数的图象如图所示: 函数y=f(x)的导函数f′(x)的图象如图所示,给出下列命题:
函数y=f(x)的导函数f′(x)的图象如图所示,给出下列命题: