题目内容
【题目】已知函数![]() (a,b
(a,b![]() R).
R).
(1)当a=b=1时,求![]() 的单调增区间;
的单调增区间;
(2)当a≠0时,若函数![]() 恰有两个不同的零点,求
恰有两个不同的零点,求![]() 的值;
的值;
(3)当a=0时,若![]() 的解集为(m,n),且(m,n)中有且仅有一个整数,求实数b的取值范围.
的解集为(m,n),且(m,n)中有且仅有一个整数,求实数b的取值范围.
【答案】(1)f(x)的单调增区间是![]() 和
和![]()
(2)![]()
(3)![]()
【解析】
(1)当a=b=1时,求得函数的导数,即可求解函数的单调区间;
(2)法一:求得![]() ,令
,令![]() ,得
,得![]() 或
或![]() ,由函数f(x)有两个不同的零点,求得
,由函数f(x)有两个不同的零点,求得![]() 的方程,即可求解;
的方程,即可求解;
法二:由![]() 得,
得,![]() ,设
,设![]() ,利用导数求得函数的单调区间和极值,进而可得函数的零点。
,利用导数求得函数的单调区间和极值,进而可得函数的零点。
(3)当![]() 时,可得
时,可得![]() ,设
,设![]() ,利用导数得到函数的单调区间和极值,转化为要使
,利用导数得到函数的单调区间和极值,转化为要使![]() 有解,和
有解,和![]() 的解集(m,n)中只有一个整数,分别列出不等式组,即可求解。
的解集(m,n)中只有一个整数,分别列出不等式组,即可求解。
(1)当a=b=1时,![]() ,
,
令![]() ,解得
,解得![]() 或
或![]()
所以f(x)的单调增区间是![]() 和
和![]()
(2)法一:![]() ,令
,令![]() ,得
,得![]() 或
或![]() ,
,
因为函数f(x)有两个不同的零点,所以![]() 或
或![]() ,
,
当![]() 时,得a=0,不合题意,舍去:
时,得a=0,不合题意,舍去:
当![]() 时,代入得
时,代入得![]()
即![]() ,所以
,所以![]() .
.
法二:由于![]() ,所以
,所以![]() ,
,
由![]() 得,
得,![]() ,
,
设![]() ,
,![]() 令
令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,h(x)递减:当
,h(x)递减:当![]() 时,
时,![]() ,
,![]() 递增
递增
当![]() 时,
时,![]() ,
,![]() 单调递增
单调递增
当![]() 时,
时, ![]() 的值域为R
的值域为R
故不论![]() 取何值,方程
取何值,方程![]() 有且仅有一个根;
有且仅有一个根;
当![]() 时,
时,![]() ,
,
所以![]() 时,方程
时,方程![]() 恰有一个根-2,
恰有一个根-2,
此时函数![]() 恰有两个零点-2和1.
恰有两个零点-2和1.
(3)当![]() 时,因为
时,因为![]() ,所以
,所以![]()
设![]() ,则
,则![]() ,
,
当![]() 时,因为
时,因为![]() ,所以
,所以![]() 在
在![]() 上递增,且
上递增,且![]() ,
,
所以在![]() 上,
上,![]() ,不合题意:
,不合题意:
当![]() 时,令
时,令![]() ,得
,得![]() ,
,
所以![]() 在
在![]() 递增,在
递增,在![]() 递减,
递减,
所以![]() ,
,
要使![]() 有解,首先要满足
有解,首先要满足![]() ,解得
,解得![]() . ①
. ①
要使![]() 的解集(m,n)中只有一个整数,则
的解集(m,n)中只有一个整数,则![]()
即![]() 解得
解得![]() . ②
. ②
设![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 递增:当
递增:当![]() 时,
时,![]() ,
,![]() 递减
递减
所以![]() ,所以
,所以![]() ,
,
所以由①和②得,![]() .
.

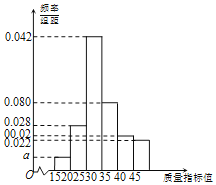
【题目】为保障食品安全,某地食品药监管部门对辖区内甲、乙两家食品企业进行检查,分别从这两家企业生产的某种同类产品中随机抽取了100件作为样本,并以样本的一项关键质量指标值为检测依据.已知该质量指标值对应的产品等级如下:
质量指标值 | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) | [40,45] |
等级 | 次品 | 二等品 | 一等品 | 二等品 | 三等品 | 次品 |
根据质量指标值的分组,统计得到了甲企业的样本频率分布直方图和乙企业的样本频数分布表(如下面表,其中a>0).
质量指标值 | 频数 |
[15,20) | 2 |
[20,25) | 18 |
[25,30) | 48 |
[30,35) | 14 |
[35,40) | 16 |
[40,45] | 2 |
合计 | 100 |
(Ⅰ)现从甲企业生产的产品中任取一件,试估计该件产品为次品的概率;
(Ⅱ)为守法经营、提高利润,乙企业开展次品生产原因调查活动.已知乙企业从样本里的次品中随机抽取了两件进行分析,求这两件次品中恰有一件指标值属于[40,45]的产品的概率;
(Ⅲ)根据图表数据,请自定标准,对甲、乙两企业食品质量的优劣情况进行比较.
【题目】“工资条里显红利,个税新政人民心”,随着2019年新年钟声的敲响,我国自1980年以来,力度最大的一次个人所得税(简称个税)改革迎来了全面实施的阶段,某![]() 从业者为了解自己在个税新政下能享受多少税收红利,绘制了他在26岁~35岁(2009年~2018年)之间各月的月平均收入
从业者为了解自己在个税新政下能享受多少税收红利,绘制了他在26岁~35岁(2009年~2018年)之间各月的月平均收入![]() (单位:千元)的散点图:
(单位:千元)的散点图:
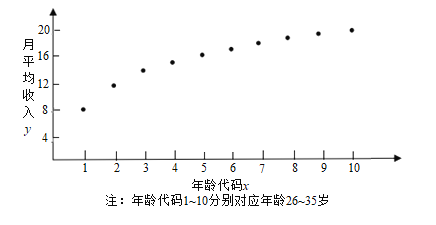
(1)由散点图知,可用回归模型![]() 拟合
拟合![]() 与
与![]() 的关系,试根据有关数据建立
的关系,试根据有关数据建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)如果该![]() 从业者在个税新政下的专项附加扣除为3000元/月,试利用(1)的结果,将月平均收入为月收入,根据新旧个税政策,估计他36岁时每个月少缴交的个人所得税.
从业者在个税新政下的专项附加扣除为3000元/月,试利用(1)的结果,将月平均收入为月收入,根据新旧个税政策,估计他36岁时每个月少缴交的个人所得税.
附注:
参考数据![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ;取
;取![]() ,
,![]()
参考公式:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为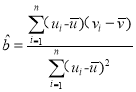 ,
,![]()
新旧个税政策下每月应纳税所得额(含税)计算方法及税率表如下:
旧个税税率表(个税起征点3500元) | 新个税税率表(个税起征点5000元) | |||
税缴级数 | 每月应纳税所得额(含税) =收入-个税起征点 | 税率 (%) | 每月应纳税所得额(含税) =收入一个税起征点-专项附加扣除 | 税率 (%) |
1 | 不超过1500元的部分 | 3 | 不超过3000元的部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 超过12000元至25000元的部分 | 20 |
4 | 超过9000元至35000元的部分 | 25 | 超过25000元至35000元的部分 | 25 |
5 | 超过35000元155000元的部分 | 30 | 超过35000元至55000元的部分 | 30 |