题目内容
6. 如图,已知扇形AOP的半径为1,圆心角大小为$\frac{π}{3}$,等腰梯形ABCD是扇形AOP的内接梯形,顶点C,D分别在OP,OA上.顶点B在弧AP上,设∠AOB=θ.
如图,已知扇形AOP的半径为1,圆心角大小为$\frac{π}{3}$,等腰梯形ABCD是扇形AOP的内接梯形,顶点C,D分别在OP,OA上.顶点B在弧AP上,设∠AOB=θ.(1)求出用θ表示等腰梯形ABCD的面积S的函数关系式;
(2)是否存在面积为$\frac{\sqrt{3}}{6}$的等腰梯形ABCD,若存在,求出此时梯形的高,若不存在,请说明理由.
分析 (1)利用已知条件,求出梯形的底边与高的长度,然后表示出梯形的面积.
(2)通过面积的值,求解正弦函数值,也就是梯形的高.推出结果即可.
解答 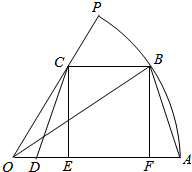 解:(1)作BF⊥AD于F,CE⊥A于E,
解:(1)作BF⊥AD于F,CE⊥A于E,
则OF=cosθ,BF=sinθ,AF=1-cosθ,BC=OF-OE=cosθ-$\frac{sinθ}{tan\frac{π}{3}}$=cosθ-$\frac{\sqrt{3}}{3}sinθ$,
AD=BC+2AF=cosθ-$\frac{\sqrt{3}}{3}sinθ$+2(1-cosθ)=2-cosθ-$\frac{\sqrt{3}}{3}sinθ$,
S=$\frac{AD+CB}{2}×BF$=$\frac{(cosθ-\frac{\sqrt{3}}{3}sinθ+2-cosθ-\frac{\sqrt{3}}{3}sinθ)}{2}×sinθ$
=$(1-\frac{\sqrt{3}}{3}sinθ)sinθ$.$θ∈(0,\frac{π}{3})$.
(2)存在面积为$\frac{\sqrt{3}}{6}$的等腰梯形ABCD,可得$(1-\frac{\sqrt{3}}{3}sinθ)sinθ=\frac{\sqrt{3}}{6}$,
可得-$\frac{\sqrt{3}}{3}{sin}^{2}θ+sinθ-\frac{\sqrt{3}}{6}=0$,
即:${2sin}^{2}θ-2\sqrt{3}sinθ+1=0$,
解得sin$θ=\sqrt{3}-1$,sinθ=$\sqrt{3}+1$(舍去).
此时梯形的高:$\sqrt{3}-1$.
点评 本题考查函数的几何中的应用,三角函数的应用,三角方程的解法,考查计算能力.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
18.设i为虚数单位,则复数2-i的模为( )
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | 3 | D. | 1 |