题目内容
(本小题12分)设 ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量 ,向量
,向量 ,
, ,动点
,动点 的轨迹为E. 求轨迹E的方程,并说明该方程所表示曲线的形状.
的轨迹为E. 求轨迹E的方程,并说明该方程所表示曲线的形状.
即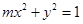 .
.
当m=0时,方程表示两直线,方程为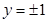 ;
;
当 时, 方程表示的是圆
时, 方程表示的是圆
当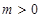 且
且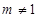 时,方程表示的是椭圆;
时,方程表示的是椭圆;
当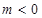 时,方程表示的是双曲线.
时,方程表示的是双曲线.
解析试题分析:根据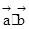 得到
得到 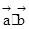 =0可求关于动点M(x,y)的方程,由圆锥曲线的性质对k进行讨论即可.
=0可求关于动点M(x,y)的方程,由圆锥曲线的性质对k进行讨论即可.
解:(1)因为 ,
, ,
, ,
,
所以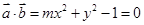 , 即
, 即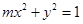 .
.
当m=0时,方程表示两直线,方程为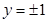 ;
;
当 时, 方程表示的是圆
时, 方程表示的是圆
当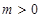 且
且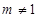 时,方程表示的是椭圆;
时,方程表示的是椭圆;
当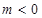 时,方程表示的是双曲线.
时,方程表示的是双曲线.
考点:本题主要考查了利用向量垂直关系,即其数量积为零来得到轨迹方程。
点评:解决该试题的关键是对于得到的关系式表示的轨迹的情况讨论是否完备,注意对于m=0的情况的讨论,遗漏问题时该题的一个易错点。

练习册系列答案
相关题目
 及直线
及直线 .
. 为何值时,直线与椭圆有公共点?
为何值时,直线与椭圆有公共点? ,求直线的方程.
,求直线的方程. 轴上,椭圆短轴的端点和焦点组成的四边形为正方形,且
轴上,椭圆短轴的端点和焦点组成的四边形为正方形,且 .
. 过点
过点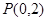 ,且与椭圆相交于
,且与椭圆相交于 、
、 不同的两点,当
不同的两点,当 面积取得最大值时,求直线
面积取得最大值时,求直线 :
: (
( )的离心率
)的离心率 ,直线
,直线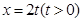 与椭圆
与椭圆 ,以线段
,以线段 为直径作圆
为直径作圆 ,圆心为
,圆心为 轴相切的时候,求
轴相切的时候,求 的值;
的值; 为坐标原点,求
为坐标原点,求 面积的最大值。
面积的最大值。 与直线
与直线 交于两个不同的点
交于两个不同的点 ,求双曲线
,求双曲线 的离心率
的离心率 的取值范围.
的取值范围. 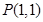 为椭圆
为椭圆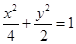 内的一定点,过P点引一直线,与椭圆相交于
内的一定点,过P点引一直线,与椭圆相交于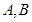 两点,且P恰好为弦AB的中点,如图所示,求弦AB所在的直线方程及弦AB的长度。
两点,且P恰好为弦AB的中点,如图所示,求弦AB所在的直线方程及弦AB的长度。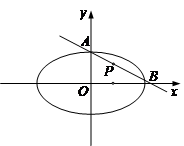
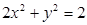 的一个焦点的直线交椭圆于
的一个焦点的直线交椭圆于 、
、 两点,求
两点,求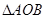 面积的最大值.(
面积的最大值.( 为坐标原点)
为坐标原点)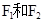 在坐标轴上,离心率为
在坐标轴上,离心率为 ,且过点(4,-
,且过点(4,- )(1)求双曲线的方程.(2)若点M(3,m)在双曲线上,求证:
)(1)求双曲线的方程.(2)若点M(3,m)在双曲线上,求证: .(3)若点A,B在双曲线上,点N(3,1)恰好是AB的中点,求直线AB的方程(12分)
.(3)若点A,B在双曲线上,点N(3,1)恰好是AB的中点,求直线AB的方程(12分) 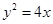 的焦点为
的焦点为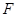 ,过点
,过点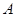 ,
,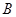 两点.
两点.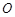 为坐标原点,求证:
为坐标原点,求证: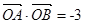 ;
;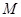 在线段
在线段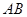 上运动,原点
上运动,原点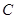 ,求四边形
,求四边形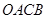 面积的最小值..
面积的最小值..