题目内容
(12分)过椭圆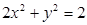 的一个焦点的直线交椭圆于
的一个焦点的直线交椭圆于 、
、 两点,求
两点,求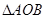 面积的最大值.(
面积的最大值.( 为坐标原点)
为坐标原点)
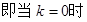 ,
,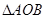 面积最大,且最大值为
面积最大,且最大值为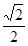 。
。
解析试题分析: 由对称性不妨设直线
由对称性不妨设直线 的方程为
的方程为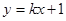 代入椭圆方程消y得
代入椭圆方程消y得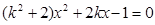
然后利用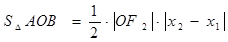 ,再借助韦达定理表示出S关于k的函数关系式,再利用基本不等式求最值即可.
,再借助韦达定理表示出S关于k的函数关系式,再利用基本不等式求最值即可.
由已知: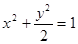 ,
, 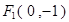
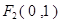 ,
, 由对称性不妨设直线
由对称性不妨设直线 的方程为
的方程为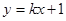
与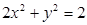 联立消去
联立消去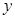 得:
得: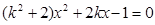 ………6分
………6分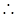
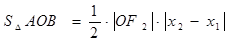
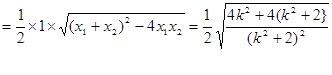 ………8分
………8分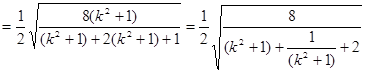 ………10分
………10分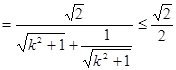 当且仅当
当且仅当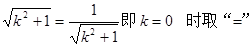
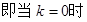 ,
,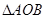 面积最大,且最大值为
面积最大,且最大值为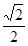 ………12分
………12分
考点:直线与椭圆的位置关系,函数最值,基本不等式求最值.
点评:解本小题的关键是建立S关于直线斜率k的函数关系式,方法是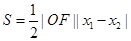 ,再借助韦达定理即可得到.
,再借助韦达定理即可得到.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 的离心率为2,坐标原点到
的离心率为2,坐标原点到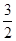 ,其中A
,其中A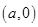 ,B
,B .
.  是双曲线虚轴在
是双曲线虚轴在 轴正半轴上的端点,过
轴正半轴上的端点,过 两点,求
两点,求 时,直线
时,直线 的方程.
的方程. ,一个焦点是F(0,1).
,一个焦点是F(0,1). 过点F交椭圆于A、B两点,且
过点F交椭圆于A、B两点,且 ,求直线
,求直线 ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量 ,向量
,向量 ,
, ,动点
,动点 的轨迹为E. 求轨迹E的方程,并说明该方程所表示曲线的形状.
的轨迹为E. 求轨迹E的方程,并说明该方程所表示曲线的形状. 均在椭圆
均在椭圆 上,直线
上,直线 分别过椭圆的左、右焦点
分别过椭圆的左、右焦点 当
当 时,有
时,有
 的方程
的方程 是椭圆
是椭圆 为圆
为圆 的任一条直径,求
的任一条直径,求 的最大值
的最大值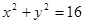 上的一个动点,过点P作PD垂直于
上的一个动点,过点P作PD垂直于 轴,垂足为D,Q为线段PD的中点。
轴,垂足为D,Q为线段PD的中点。 有相同的焦点,求此双曲线的标准方程.
有相同的焦点,求此双曲线的标准方程. 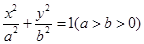 的一个焦点
的一个焦点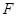 与抛物线
与抛物线 的焦点重合,P为椭圆与抛物线的一个公共点,且|PF|=2,倾斜角为
的焦点重合,P为椭圆与抛物线的一个公共点,且|PF|=2,倾斜角为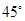 的直线
的直线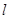 过点
过点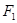 ,问抛物线
,问抛物线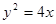 上是否存在一点
上是否存在一点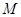 ,使得
,使得 的离心率为2,坐标原点到直线AB的距离为
的离心率为2,坐标原点到直线AB的距离为 ,其中A
,其中A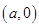 ,B
,B .
.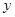 轴正半轴上的端点,过B1作直线与双曲线交于
轴正半轴上的端点,过B1作直线与双曲线交于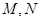 两点,求
两点,求 时,直线
时,直线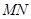 的方程.
的方程.