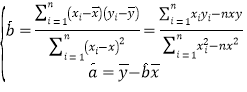题目内容
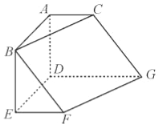
【题目】如图,在六面体![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,且
,且![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)设DG的中点为M,连结AM,FM,则DEFM是平行四边形,从而MF∥DE,且MF=DE,进而AB∥DE,推导出四边形ABFM是平行四边形,从而BF∥AM,由此能证明BF∥平面ACGD.
(2)以DE,DG,DA分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角D﹣CG﹣F的余弦值.
(1)证明:设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,则
,则![]() 是平行四边形,
是平行四边形,
所以![]() 且
且![]() ,因为平面
,因为平面![]() 平面
平面![]() ,
,
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() ,因为
,因为![]() ,所以
,所以![]() 且
且![]() ,
,
所以四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
故![]() 平面
平面![]() .
.
(2)由题意可得:![]() 两两垂直,故以
两两垂直,故以![]() 分别为
分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,令
轴建立空间直角坐标系,令![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,设平面
,设平面![]() 的法向量
的法向量![]() ,则
,则
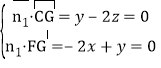 ,令
,令![]() ,则
,则![]() ,
,
因为平面![]() 的法向量
的法向量![]() ,
,
所以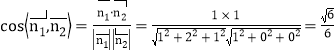
由于所求二面角为锐二面角,所以二面角![]() 的余弦值为
的余弦值为![]() .
.


练习册系列答案
相关题目
【题目】某种设备随着使用年限的增加,每年的维护费相应增加.现对一批该设备进行调查,得到这批设备自购入使用之日起,前5年平均每台设备每年的维护费用大致如表:
年份 |
|
|
|
|
|
维护费 |
|
|
|
|
|
(I)从这![]() 年中随机抽取两年,求平均每台设备每年的维护费用至少有
年中随机抽取两年,求平均每台设备每年的维护费用至少有![]() 年多于
年多于![]() 万元的概率;
万元的概率;
(II)求![]() 关于
关于![]() 的线性回归方程;若该设备的价格是每台
的线性回归方程;若该设备的价格是每台![]() 万元,你认为应该使用满五年换一次设备,还是应该使用满八年换一次设备?并说明理由.
万元,你认为应该使用满五年换一次设备,还是应该使用满八年换一次设备?并说明理由.
参考公式:用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式: