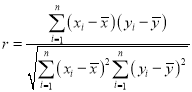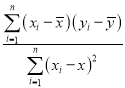题目内容
【题目】
是双曲线
的右支上一点，
分别为双曲线的左右焦点,则
的内切圆的圆心横坐标为（ ）
A. 
B. 2C. 
D. 3
【答案】A
【解析】
设内切圆与x轴的切点是点H，根据切线长定理和双曲线的定义，把|PF1|﹣|PF2|＝2
，转化为|HF1|﹣|HF2|＝2，从而求得点H的横坐标．
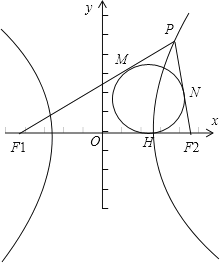
如图所示：F1（﹣
，0）、F2（，0），设内切圆与x轴的切点是点H，PF1、PF2与内切圆的切点分别为M、N，由双曲线的定义可得|PF1|﹣|PF2|＝2a＝2，由圆的切线长定理知，|PM|＝|PN|，
，
，故|MF1|﹣|NF2|＝2，即|HF1|﹣|HF2|＝2，设内切圆的圆心横坐标为x，即点H的横坐标为x，故 （x+）﹣（﹣x）＝2，∴x＝．
故选：A．
练习册系列答案
相关题目
