题目内容
3.如图,平面ABC⊥平面DBC,AB=AC,AB⊥AC,DB=DC;DE⊥平面DBC,BC=2DE,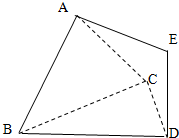
(1)求证:DE∥平面ABC;
(2)求证:AE⊥平面ABC.
分析 (1)取BC中点F,连结AF,可证AF⊥BC,由平面ABC⊥平面DBC,且交线为BC,可证AF⊥平面DBC,从而AF∥DE,即可证明DE∥平面ABC.
(2)连结DF,可证DF⊥平面ABC,AE∥DF,从而有AE⊥平面ABC.
解答 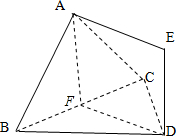 解:(1)取BC中点F,连结AF,
解:(1)取BC中点F,连结AF,
因为AB=AC,所以,AF⊥BC,
又因为平面ABC⊥平面DBC,且交线为BC,
所以,AF⊥平面DBC,
因为DE⊥平面DBC,所以,AF∥DE,
而AF在平面ABC内,DE在平面ABC外,所以,DE∥平面ABC;
(2)连结DF,
∵DB=DC,F为BC中点,
∴DF⊥BC,
∵平面ABC⊥平面DBC,DF?平面DBC,
可证DF⊥平面ABC,
∵AE∥DF,
∴AE⊥平面ABC.
点评 本题主要考查了直线与平面垂直的判定,直线与平面平行的判定,考查了空间想象能力和推理论证能力,属于基本知识的考查.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
13.有4部车床需加工3个不同的零件,不同的安排方法有多少种?( )
| A. | 34 | B. | 43 | C. | 13 | D. | 14 |
8.在5件产品中,有3件一等品和2件二等品,从中任取2件,则至多有一件一等品的概率是( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{7}{10}$ | D. | $\frac{9}{10}$ |
15.由平面内性质类比出空间几何的下列命题,你认为正确的是( )
| A. | 过直线上一点有且只有一条直线与已知直线垂直 | |
| B. | 同垂直于一条直线的两条直线互相平行 | |
| C. | 过直线外一点有且只有一条直线与已知直线平行 | |
| D. | 两组对边分别相等的四边形是平行四边形 |
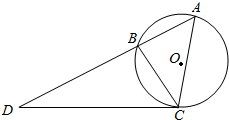
 如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC=3,AB=2$\sqrt{3}$,AC=2,
如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC=3,AB=2$\sqrt{3}$,AC=2,