题目内容
3.如图,F1、F2分别是椭圆:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的一个交点,∠F1AF2=60°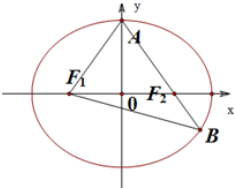
1)求椭圆C的离心率;
2)已知△AF1B的面积为40$\sqrt{3}$,求椭圆方程.
分析 (1)通过∠F1AF2=60°及对称性即得结论;
(2)通过设|BF2|=t,则|BF1|=2a-t,利用余弦定理可得t=$\frac{3}{5}$a,利用S=$\frac{1}{2}$|AF1||AB|sin60°=40$\sqrt{3}$,计算可得a2=100,进而计算可得结论.
解答 解:(1)∵∠F1AF2=60°,
∴∠F2AO=30°,
又∵△AOF2为直角三角形,
∴a=2c,
即椭圆C的离心率e=$\frac{c}{a}$=$\frac{c}{2c}$=$\frac{1}{2}$;
(2)设|BF2|=t,则|BF1|=2a-t,
又∵∠BF2F1=120°,|F1F2|=2c,
∴|BF1|2=|BF2|2+|F1F2|2-2|BF2||F1F2|cos120°
即(2a-t)2=t2+a2+at,
整理得:3a2=5at,
∴t=$\frac{3}{5}$a,
∵△AF1B面积S=40$\sqrt{3}$,
∴$\frac{1}{2}$|AF1||AB|sin60°=40$\sqrt{3}$,
即$\frac{1}{2}$•a•(a+$\frac{3}{5}$a)•$\frac{\sqrt{3}}{2}$=40$\sqrt{3}$,
整理得:a2=100,
解得:a=10,
∴c=$\frac{1}{2}$a=5,b2=a2-c2=100-25=75,
∴椭圆方程为:$\frac{{x}^{2}}{100}+\frac{{y}^{2}}{75}=1$.
点评 本题考查椭圆的简单性质,涉及余弦定理、三角形面积公式等基础知识,注意解题方法的积累,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列命题中,真命题是( )
| A. | ?x0∈R,e${\;}^{{x}_{0}}$≤0 | B. | ?x∈R,2x>x2 | ||
| C. | 命题:若x≠y,则sinx≠siny逆否命题 | D. | a>1,b>1是ab>1的充分不必要条件 |
12.已知x1<x2且函数f(x)=$\frac{1}{3}$ax3+$\frac{1}{2}$bx2-x+1的极大值为f(x1)、极小值为f(x2),又x1,x2中至少有一个数在区间(1,2)内,则a-b的取值范围为( )
| A. | (-2,+∞) | B. | (-∞,-2) | C. | (-∞,2) | D. | (-2,2) |