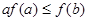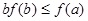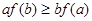题目内容
已知函数f(x)=ax-x3,对区间(0,1)上的任意x1,x2,且x1<x2,都有f(x2)-f(x1)>x2-x1成立,则实数a的取值范围为( )
| A.(0,1) | B.[4,+∞) | C.(0,4] | D.(1,4] |
B
解析

练习册系列答案
相关题目
函数 =
= 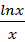 的最大值为( )
的最大值为( )
A.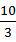 | B.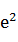 | C.e | D. |
等比数列 中,
中, ,前3项和为
,前3项和为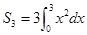 ,则公q的值是( )
,则公q的值是( )
| A. 1 | B.- | C. 1或- | D.- 1或- |
设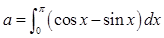 ,则二项式
,则二项式 展开式中的
展开式中的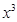 项的系数为( )
项的系数为( )
| A.20 | B.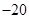 | C.160 | D. |
已知f(x)是定义域为R的奇函数,f(-4)=-1,f(x)的导函数f′(x)的图像如图X18-1所示.若两正数a,b满足f(a+2b)<1,则 的取值范围是( )
的取值范围是( )
A.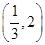 | B.(-∞,-1) | C.(-1,0) | D. |
函数f(x)的定义域为(0,+∞),且f(x)>0,f′(x)>0,则函数y=xf(x)( )
| A.存在极大值 | B.存在极小值 |
| C.是增函数 | D.是减函数 |
若S1=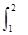 x2dx,S2=
x2dx,S2=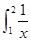 dx,S3=
dx,S3=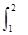 exdx,则S1,S2,S3的大小关系为( ).
exdx,则S1,S2,S3的大小关系为( ).
| A.S1<S2<S3 | B.S2<S1<S3 |
| C.S2<S3<S1 | D.S3<S2<S1 |
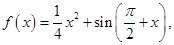
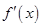 为
为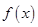 的导函数,则
的导函数,则
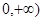 上的非负可导函数f(x)满足xf′(x)
上的非负可导函数f(x)满足xf′(x) ,对任意正数
,对任意正数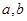 ,若满足
,若满足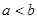 ,则必有( )
,则必有( )