题目内容
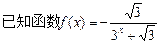
(1)求证:函数y=f(x)的图象关于点(0.5,-0.5)对称;
(2)求f(-2)+f(-1)+f(0)+f(1)+f(2)+f(3)的值;

(1)见解析(2)-3(3)见解析
(1)设P(x,y)是y=f(x)的图象上任意一点,
关于(0.5,-0.5)对称点的坐标为:(1-x,-1-y)


∴-1-y=f(1-x),即函数y=f(x)的图象关于点(0.5,-0.5)对称.
(2)由(Ⅰ)有f(1-x)=-1-f(x)即f(x)+f(1-x)= -1
∴f(-2)+f(3)=-1,f(-1)+f(2)=-1,f(0)+f(1)= -1
则f(-2)+f(-1)+f(0)+f(1)+f(2)+f(3)="-3 "

下面用数学归纳法证明
当n=1时,左=3,右=1,3>1不等式成立
当n=2时,左=9,右=4,9>4不等式成立
令n=k(k≥2)不等式成立即3k>k2
则n=k+1时,左=3k+1=3·3k>3·k2
右=(k+1)2=k2+2k+1
∵3k2-(k2+2k+1)=2k2-2k-1=2(k-0.5)2-1.5
当k≥2,k∈N时,上式恒为正值
则左>右,即3k+1>(k+1)2,所以对任何自然数n,总有3n>n2成立,即对任何自然数n,总有 bn>n2成立
bn>n2成立
关于(0.5,-0.5)对称点的坐标为:(1-x,-1-y)


∴-1-y=f(1-x),即函数y=f(x)的图象关于点(0.5,-0.5)对称.
(2)由(Ⅰ)有f(1-x)=-1-f(x)即f(x)+f(1-x)= -1
∴f(-2)+f(3)=-1,f(-1)+f(2)=-1,f(0)+f(1)= -1
则f(-2)+f(-1)+f(0)+f(1)+f(2)+f(3)="-3 "

下面用数学归纳法证明
当n=1时,左=3,右=1,3>1不等式成立
当n=2时,左=9,右=4,9>4不等式成立
令n=k(k≥2)不等式成立即3k>k2
则n=k+1时,左=3k+1=3·3k>3·k2
右=(k+1)2=k2+2k+1
∵3k2-(k2+2k+1)=2k2-2k-1=2(k-0.5)2-1.5
当k≥2,k∈N时,上式恒为正值
则左>右,即3k+1>(k+1)2,所以对任何自然数n,总有3n>n2成立,即对任何自然数n,总有
 bn>n2成立
bn>n2成立
练习册系列答案
相关题目
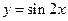 的图象向左平移
的图象向左平移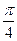 个单位, 再向上平移1个单位,所得图象的函数解析式是( )
个单位, 再向上平移1个单位,所得图象的函数解析式是( )


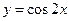
 的图像按向量
的图像按向量 平移后,得到的图像关于原点对称,则向量
平移后,得到的图像关于原点对称,则向量
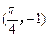

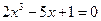 是否存在实数根.
是否存在实数根.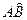 的长为
的长为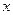 ,
,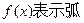
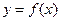 的图像是( )
的图像是( )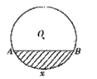
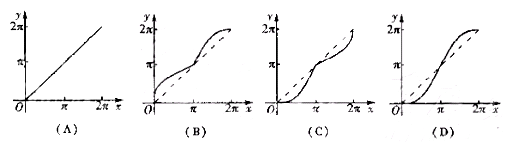

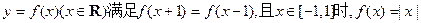 ,则函数
,则函数 的图像的交点的个数为 ( )
的图像的交点的个数为 ( )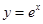 的图象与函数
的图象与函数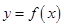 的图象关于直线
的图象关于直线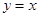 对称,则
对称,则