题目内容
19．
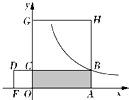如图，点B是反比例函数上一点，矩形OABC的周长是20，正方形BCGH和正方形OCDF的面积之和为68，则反比例函数的解析式是（ ）?| A． | y=$\frac{8}{x}$ | B． | y=$\frac{6}{x}$ | C． | y=-$\frac{16}{x}$ | D． | y=$\frac{16}{x}$ |
分析 设B点的坐标为（x，y）根据矩形OABC的周长是20，正方形BCGH和正方形OCDF的面积之和为68，得到x2+y2=68，x+y=10，继而求出xy=16，问题得以解决．
解答 解：设B点的坐标为（x，y），根据题意可得x2+y2=68，x+y=10，
∴xy=$\frac{1}{2}$[（x+y）2-（x2+y2）]=16，
∴y=$\frac{16}{x}$，
故选：D
点评 本题考查了函数解析式的求法，属于基础题．
练习册系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物，如图是根据某地某日早7点至晚8点甲、乙两个监测点统计的数据（单位：毫克/每立方米）列出的茎叶图，则甲、乙两地浓度的方差较小的是甲．
14．已知α为第二象限角，cos2α=-$\frac{\sqrt{5}}{3}$，则sinα-cosα=（ ）
| A． | $\frac{\sqrt{15}}{3}$ | B． | $\frac{\sqrt{15}}{3}$或$\frac{\sqrt{3}}{3}$ | C． | -$\frac{\sqrt{15}}{3}$ | D． | $\frac{\sqrt{3}}{9}$ |
11．已知12sinα-5cosα=13，则tanα=（ ）
| A． | -$\frac{5}{12}$ | B． | -$\frac{12}{5}$ | C． | ±$\frac{12}{5}$ | D． | ±$\frac{7}{12}$ |