题目内容
10.对于定义域为D的函数y=f(x)和常数c,若对任意正实数ξ,?x∈D使得0<|f(x)-c|<ξ恒成立,则称函数y=f(x)为“敛c函数”.现给出如下函数:①f(x)=x(x∈Z)
②$f(x)={({\frac{1}{2}})^x}+1({x∈Z})$
③f(x)=log2x
④$f(x)=\frac{x-1}{x}$.其中为“敛1函数”的有( )
| A. | ①② | B. | ③④ | C. | ②③④ | D. | ①②③ |
分析 由“敛C函数”的定义可知,当自变量x趋近于某个值或无穷大时,函数值y无限趋近于一个常数C,由此性质对四个函数逐一判断.
解答 解:对于函数①,取ξ=$\frac{1}{3}$,因为x∈Z,找不到x,使得0<|x-1|<$\frac{1}{3}$立,所以函数①不是“敛1函数”;
对于函数②,当x→+∞时,$(\frac{1}{2})^{x}$→0,所以$(\frac{1}{2})^{x}+1$→1,所以对任意的正数ξ,总能找到一个足够大的正整数x,使得0<|f(x)-1|<ξ成立,故函数②是“敛1函数”;
对于函数③,当x→2时,log2x→log22=1,所以对于无论多大或多小的正数ξ,总会找到一个x,使得0<|f(x)-1|<ξ成立,故函数③是“敛1函数”;
对于函数④,函数式可化为y=1-$\frac{1}{x}$,所以当x→+∞时,$\frac{1}{x}$→0,即1-$\frac{1}{x}$→1,所以对于无论多小的正数ξ,总会找到一个足够大的正数x,使得0<|f(x)-1|<ξ成立,故故函数④是“敛1函数”.
故选:C.
点评 解决本题主要是对题目中新定义准确理解,解答本题中要注意已知基本函数图象的应用.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
5.已知复数Z满足$\frac{2+4i}{z}$=1-i(i为虚数单位),则复数z=( )
| A. | -1+3i | B. | -1+2i | C. | 1-3i | D. | 1-2i |
19.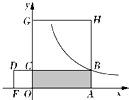 如图,点B是反比例函数上一点,矩形OABC的周长是20,正方形BCGH和正方形OCDF的面积之和为68,则反比例函数的解析式是( )?
如图,点B是反比例函数上一点,矩形OABC的周长是20,正方形BCGH和正方形OCDF的面积之和为68,则反比例函数的解析式是( )?
 如图,点B是反比例函数上一点,矩形OABC的周长是20,正方形BCGH和正方形OCDF的面积之和为68,则反比例函数的解析式是( )?
如图,点B是反比例函数上一点,矩形OABC的周长是20,正方形BCGH和正方形OCDF的面积之和为68,则反比例函数的解析式是( )?| A. | y=$\frac{8}{x}$ | B. | y=$\frac{6}{x}$ | C. | y=-$\frac{16}{x}$ | D. | y=$\frac{16}{x}$ |