题目内容
设函数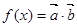 定义在
定义在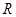 上,其中
上,其中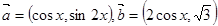 .
.
(1)求函数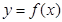 的单调递增区间;
的单调递增区间;
(2)若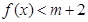 在
在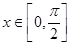 上恒成立。求实数
上恒成立。求实数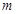 的取值范围.
的取值范围.
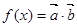 定义在
定义在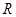 上,其中
上,其中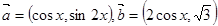 .
.(1)求函数
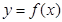 的单调递增区间;
的单调递增区间;(2)若
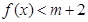 在
在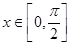 上恒成立。求实数
上恒成立。求实数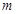 的取值范围.
的取值范围. (1)函数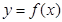 的单调递增区间为
的单调递增区间为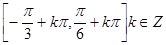 ;
;
(2)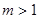 。
。
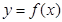 的单调递增区间为
的单调递增区间为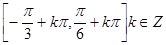 ;
;(2)
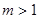 。
。本试题主要是考查了三角函数性质的运用。
(1)因为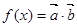
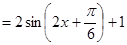 ,从而得到单调区间的求解。
,从而得到单调区间的求解。
(2)由(1)知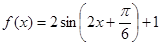
要使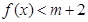 在
在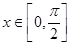 上恒成立,即
上恒成立,即
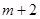 大于
大于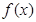 在
在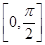 上的最大值转换为最值问题来处理。
上的最大值转换为最值问题来处理。
解: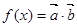
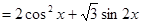
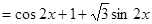
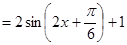 …………2分
…………2分
令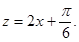 函数
函数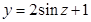 的单调递增区间是
的单调递增区间是
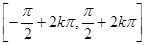
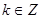
由
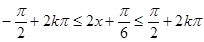 ,
,
得
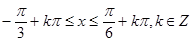 …………5分
…………5分
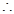 函数
函数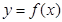 的单调递增区间为
的单调递增区间为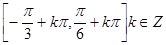 …………6分
…………6分
(2)由(1)知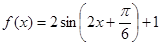
要使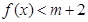 在
在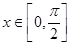 上恒成立,即
上恒成立,即
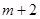 大于
大于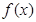 在
在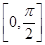 上的最大值………8分
上的最大值………8分
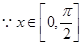
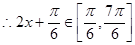
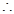 当
当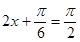 时,即
时,即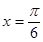 时,
时,
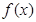 有最大值,
有最大值,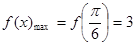
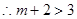 即
即 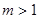 ………12分
………12分
(1)因为
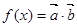
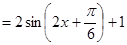 ,从而得到单调区间的求解。
,从而得到单调区间的求解。 (2)由(1)知
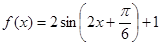
要使
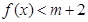 在
在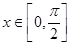 上恒成立,即
上恒成立,即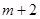 大于
大于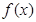 在
在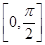 上的最大值转换为最值问题来处理。
上的最大值转换为最值问题来处理。解:
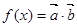
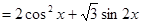
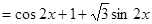
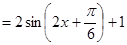 …………2分
…………2分令
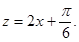 函数
函数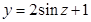 的单调递增区间是
的单调递增区间是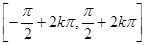
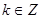
由
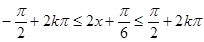 ,
,得
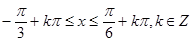 …………5分
…………5分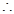 函数
函数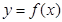 的单调递增区间为
的单调递增区间为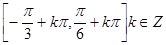 …………6分
…………6分(2)由(1)知
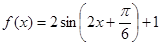
要使
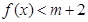 在
在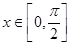 上恒成立,即
上恒成立,即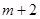 大于
大于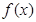 在
在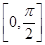 上的最大值………8分
上的最大值………8分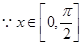
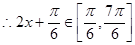
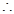 当
当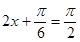 时,即
时,即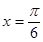 时,
时,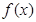 有最大值,
有最大值,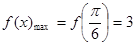
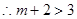 即
即 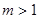 ………12分
………12分 
练习册系列答案
相关题目
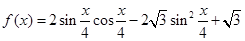 .
.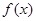 的最小正周期及最值; (Ⅱ)令
的最小正周期及最值; (Ⅱ)令 ,判断函数
,判断函数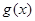 的奇偶性,并说明理由.
的奇偶性,并说明理由. 
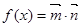 ,其中向量
,其中向量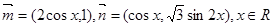 ,
,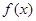 的最小正周期;
的最小正周期;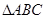 中,
中,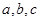 分别是角
分别是角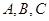 的对边,
的对边,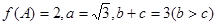 求
求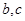 的值.
的值.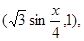 n=
n=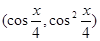 .
.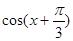 的值;
的值;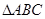 中,角A,B,C的对边分别是a,b,c,且满足
中,角A,B,C的对边分别是a,b,c,且满足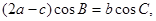 求f(A)的取值范围.
求f(A)的取值范围. 
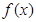 的最小正周期T;
的最小正周期T;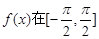 上的图象;
上的图象;
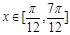 时,f (x)的反函数为
时,f (x)的反函数为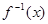 ,
,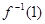 的值.
的值. 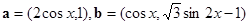 ,设函数
,设函数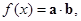 其中xÎR.
其中xÎR.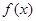 的最小正周期和单调递增区间.
的最小正周期和单调递增区间.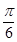 个单位得到
个单位得到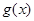 的图象,求
的图象,求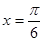 是函数
是函数 图象的一条对称轴,当
图象的一条对称轴,当 取最小正数时( )
取最小正数时( )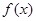 在
在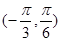 单调递减
单调递减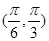 单调递增
单调递增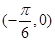 单调递减
单调递减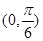 单调递增
单调递增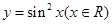 的最小正周期为
的最小正周期为
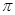
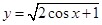 的定义域是 ( )
的定义域是 ( )


