题目内容
已知双曲线C:2x2-y2=2与点P(1,2).求过点P(1,2)的直线l的斜率k的取值范围,使l与C只有一个交点;
当k=±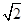 或k=
或k=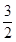 或k不存在时,l与C只有一个交点.
或k不存在时,l与C只有一个交点.
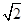 或k=
或k=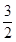 或k不存在时,l与C只有一个交点.
或k不存在时,l与C只有一个交点.本试题主要是考查了直线与双曲线的位置关系的综合运用。根据已知中的曲线方程和点P的坐标,设出直线方程,然后联立方程组,进而结合方程有一个解,得到参数k的范围和参数k的值。
解:设直线l的方程为y-2=k(x-1),
代入双曲线C的方程,整理得
(2-k2)x2+2(k2-2k)x-k2+4k-6=0(*)
当2-k2=0,即k=±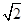 时,直线与双曲线的渐近线平行,此时只有一个交点.
时,直线与双曲线的渐近线平行,此时只有一个交点.
②当2-k2≠0时,令Δ=0,得k=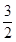 .此时只有一个公共点.
.此时只有一个公共点.
又点(1,2)与双曲线的右顶点(1,0)在直线x=1上,而x=1为双曲线的一条切线.
∴当k不存在时,直线与双曲线只有一个公共点.
综上所述,当k=±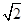 或k=
或k=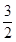 或k不存在时,l与C只有一个交点.
或k不存在时,l与C只有一个交点.
解:设直线l的方程为y-2=k(x-1),
代入双曲线C的方程,整理得
(2-k2)x2+2(k2-2k)x-k2+4k-6=0(*)
当2-k2=0,即k=±
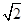 时,直线与双曲线的渐近线平行,此时只有一个交点.
时,直线与双曲线的渐近线平行,此时只有一个交点.②当2-k2≠0时,令Δ=0,得k=
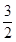 .此时只有一个公共点.
.此时只有一个公共点.又点(1,2)与双曲线的右顶点(1,0)在直线x=1上,而x=1为双曲线的一条切线.
∴当k不存在时,直线与双曲线只有一个公共点.
综上所述,当k=±
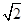 或k=
或k=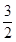 或k不存在时,l与C只有一个交点.
或k不存在时,l与C只有一个交点. 
练习册系列答案
相关题目
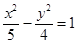 的焦点为
的焦点为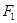 、
、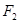 ,点
,点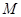 在双曲线上且
在双曲线上且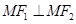 ,则点
,则点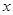 轴的距离为 .
轴的距离为 . 为双曲线
为双曲线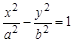 的左右焦点,点P在双曲线的左支上,且
的左右焦点,点P在双曲线的左支上,且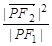 的最小值为
的最小值为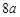 ,则双曲线的离心率的取值范围是 .
,则双曲线的离心率的取值范围是 .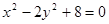 的焦点坐标为
的焦点坐标为 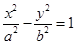 (
(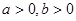 )的两个焦点为
)的两个焦点为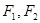 ,若双曲线上存在一点
,若双曲线上存在一点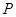 ,满足
,满足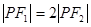 ,则双曲线离心率的取值范围为
,则双曲线离心率的取值范围为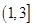
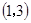
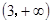
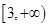
 ,离心率为
,离心率为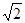 ,且过点(5,4),则其焦距为
,且过点(5,4),则其焦距为 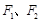 分别是双曲线
分别是双曲线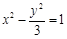 的两个焦点,P是该双曲线上的一点,且
的两个焦点,P是该双曲线上的一点,且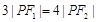 ,则
,则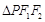 的面积等于
的面积等于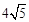
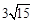
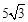
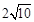
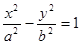
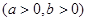 的一条渐近线方程为
的一条渐近线方程为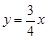 ,则此双曲线的离心率为( )
,则此双曲线的离心率为( )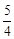
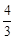
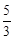
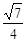
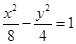 的离心率为 .
的离心率为 .