题目内容
已知双曲线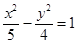 的焦点为
的焦点为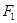 、
、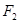 ,点
,点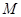 在双曲线上且
在双曲线上且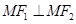 ,则点
,则点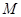 到
到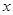 轴的距离为 .
轴的距离为 .
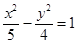 的焦点为
的焦点为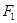 、
、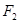 ,点
,点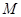 在双曲线上且
在双曲线上且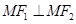 ,则点
,则点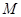 到
到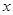 轴的距离为 .
轴的距离为 .
试题分析:设
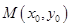 ,由双曲线的定义知:
,由双曲线的定义知: ………………①
………………①又
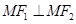 ,所以
,所以 ………………………………②
………………………………②由①②得
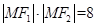 ,
,在
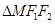 中,
中,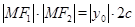 ,所以
,所以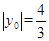 ,所以点
,所以点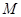 到
到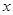 轴的距离为
轴的距离为 。
。点评:此题求“点
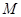 到
到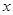 轴的距离”,实质上就是求点M的纵坐标,我们利用双曲线的定义和勾股定理相结合来求得。
轴的距离”,实质上就是求点M的纵坐标,我们利用双曲线的定义和勾股定理相结合来求得。
练习册系列答案
相关题目
题目内容
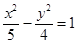 的焦点为
的焦点为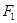 、
、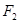 ,点
,点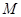 在双曲线上且
在双曲线上且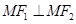 ,则点
,则点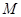 到
到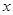 轴的距离为 .
轴的距离为 .
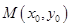 ,由双曲线的定义知:
,由双曲线的定义知: ………………①
………………①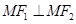 ,所以
,所以 ………………………………②
………………………………②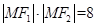 ,
,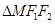 中,
中,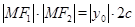 ,所以
,所以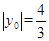 ,所以点
,所以点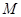 到
到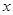 轴的距离为
轴的距离为 。
。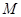 到
到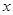 轴的距离”,实质上就是求点M的纵坐标,我们利用双曲线的定义和勾股定理相结合来求得。
轴的距离”,实质上就是求点M的纵坐标,我们利用双曲线的定义和勾股定理相结合来求得。