题目内容
用反证法证明命题:若P则q ,其第一步是反设命题的结论不成立,这个正确的反设是
| A.若P则非q | B.若非P则q | C.非P | D.非q |
D
对“若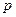 则
则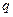 ”的否定已经不是“四种命题”中的任何一种,而是表示“合取”命题;
”的否定已经不是“四种命题”中的任何一种,而是表示“合取”命题;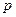 且非
且非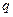 ,即反设命题的结论不成立为非
,即反设命题的结论不成立为非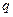 ,选D。
,选D。
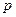 则
则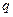 ”的否定已经不是“四种命题”中的任何一种,而是表示“合取”命题;
”的否定已经不是“四种命题”中的任何一种,而是表示“合取”命题;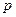 且非
且非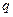 ,即反设命题的结论不成立为非
,即反设命题的结论不成立为非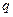 ,选D。
,选D。
练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 ”命题:
”命题: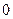 的两个实数都为
的两个实数都为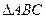 是锐角三角形, 则
是锐角三角形, 则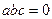 ,则
,则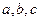 中至少有一个为
中至少有一个为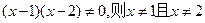 。
。 :
: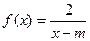 在区间
在区间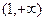 上是减函数;命题
上是减函数;命题 :
: 是方程
是方程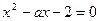 的两个实根,不等式
的两个实根,不等式 对任意实数
对任意实数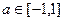 恒成立;若
恒成立;若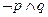 为真,试求实数
为真,试求实数 的取值范围。
的取值范围。 :方程
:方程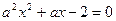 在
在 上有且仅有一解;命题
上有且仅有一解;命题 :只有一个实数
:只有一个实数 满足不等式
满足不等式 若命题
若命题 是假命题,求
是假命题,求 的取值范围.
的取值范围.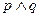 ” 形式
” 形式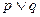 ”形式
”形式 ,命题Q:
,命题Q: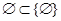 ,那么下列结论不正确的是
,那么下列结论不正确的是 是定义在区间
是定义在区间 上的偶函数,命题
上的偶函数,命题 :
: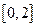 上单调递减;命题
上单调递减;命题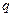 :
: ,若“
,若“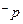 或
或 的取值范围。
的取值范围。 ,
,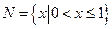 ,那么“
,那么“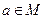 ”是“
”是“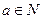 ”的()
”的()