题目内容
10.已知$sinx=\frac{{\sqrt{3}}}{5}(\frac{π}{2}<x<π)$,则x的值( )| A. | $arcsin\frac{{\sqrt{3}}}{5}$ | B. | arcsin(-$\frac{\sqrt{3}}{5}$) | C. | π-arcsin$\frac{{\sqrt{3}}}{5}$ | D. | $\frac{π}{2}+arcsin\frac{{\sqrt{3}}}{5}$ |
分析 由条件利用反正弦函数的定义、诱导公式求得x的值.
解答 解:根据已知$sinx=\frac{{\sqrt{3}}}{5}(\frac{π}{2}<x<π)$,
arcsin$\frac{\sqrt{3}}{5}$表示在[0,$\frac{π}{2}$]上正弦值等于$\frac{\sqrt{3}}{5}$的一个角,π-arcsin$\frac{\sqrt{3}}{5}$∈(0,$\frac{π}{2}$),
且sin[π-arcsin$\frac{\sqrt{3}}{5}$]=sin(arcsin$\frac{\sqrt{3}}{5}$)=$\frac{\sqrt{3}}{5}$,
∴x=π-arcsin$\frac{\sqrt{3}}{5}$,
故选:C.
点评 本题主要考查反正弦函数的定义,诱导公式的应用,属于基础题.

练习册系列答案
相关题目
18.已知向量$\overrightarrow{a}$=(3,4),$\overrightarrow{b}$=(-3,1),$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ,则tanθ等于( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | -3 | D. | 3 |
15.若动点M(x,y)在运动过程中,总满足关系式$\sqrt{{{(x+5)}^2}+{y^2}}-\sqrt{{{(x-5)}^2}+{y^2}}$=8,则M的轨迹为( )
| A. | 椭圆$\frac{x^2}{25}+\frac{y^2}{16}$=1 | B. | 双曲线$\frac{x^2}{16}-\frac{y^2}{9}$=1的右支 | ||
| C. | 双曲线$\frac{x^2}{9}-\frac{y^2}{16}$=1的右支 | D. | 双曲线$\frac{x^2}{16}-\frac{y^2}{9}$=1的左支 |
19.已知集合M={a,b,c},集合A={x|x⊆M},则集合A有几个元素( )
| A. | 3 | B. | 6 | C. | 7 | D. | 8 |
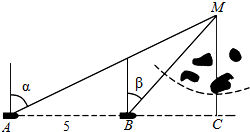 如图,一船由西向东航行,在A处测得某岛M的方位角为α,前进5km后到达B处,测得岛M的方位角为β.已知该岛周围3km内有暗礁,现该船继续东行.
如图,一船由西向东航行,在A处测得某岛M的方位角为α,前进5km后到达B处,测得岛M的方位角为β.已知该岛周围3km内有暗礁,现该船继续东行. 由曲线y=sinx,y=cosx与直线x=0,x=$\frac{π}{2}$所围成的平面图形(下图中的阴影部分)的面积是2$\sqrt{2}$-2.
由曲线y=sinx,y=cosx与直线x=0,x=$\frac{π}{2}$所围成的平面图形(下图中的阴影部分)的面积是2$\sqrt{2}$-2.