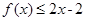题目内容
已知函数 在
在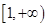 上为增函数,且
上为增函数,且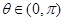 ,
,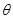 为常数,
为常数,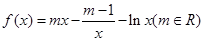 .
.
(1)求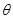 的值;
的值;
(2)若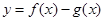 在
在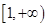 上为单调函数,求
上为单调函数,求 的取值范围;
的取值范围;
(3)设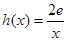 ,若在
,若在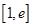 上至少存在一个
上至少存在一个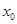 ,使得
,使得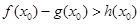 成立,求
成立,求 的取值范围.
的取值范围.
(1) (2)
(2) (3)
(3) 
解析试题分析:(1)由题意: 在
在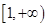 上恒成立,即
上恒成立,即
在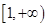 上恒成立,
上恒成立,
只需sin
(2) 由(1),得f(x)-g(x)= -
- ,
, ,由于f(x)-g(x)在其定义域内为单调函数,则
,由于f(x)-g(x)在其定义域内为单调函数,则 在
在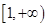 上恒成立,即
上恒成立,即 在
在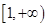 上恒成立,故
上恒成立,故 ,综上,m的取值范围是
,综上,m的取值范围是
(3)构造函数F(x)=f(x)-g(x)-h(x), ,
,
当 由
由 得,
得, ,所以在
,所以在 上不存在一个
上不存在一个 ,使得
,使得 ;
;
当m>0时, ,因为
,因为 ,所以
,所以 在
在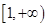 上恒成立,故F(x)在
上恒成立,故F(x)在 上单调递增,
上单调递增, ,故m的取值范围是
,故m的取值范围是
另法:(3) 令
令


考点:导数的运算性质,恒成立问题,构造函数思想。
点评:本题综合运用导数性质,恒成立思想,构造函数思想综合求出 的范围。
的范围。

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
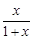 .
.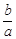 .
. ,
, ,
, 所围成的平面图形的面积。
所围成的平面图形的面积。 .
.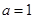 时,试判断
时,试判断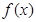 的单调性并给予证明;
的单调性并给予证明;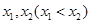 .
.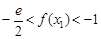 。 (注:
。 (注: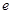 是自然对数的底数)
是自然对数的底数) ,
, 的单调区间和极值点;
的单调区间和极值点; ,记过点
,记过点 与原点的直线斜率为
与原点的直线斜率为 。是否存在
。是否存在 使
使 ?若存在,求出
?若存在,求出 (a为实常数).
(a为实常数).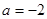 ,求证:函数
,求证:函数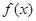 在(1,+.∞)上是增函数;
在(1,+.∞)上是增函数;  值;
值;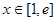 ,使得
,使得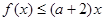 成立,求实数a的取值范围.
成立,求实数a的取值范围.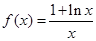 。
。 如果
如果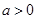 ,函数在区间
,函数在区间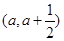 上存在极值,求实数a的取值范围;
上存在极值,求实数a的取值范围; 当
当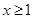 时,不等式
时,不等式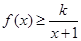 恒成立,求实数k的取值范围。
恒成立,求实数k的取值范围。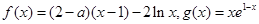 ,(
,(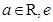 为自然对数的底数)。
为自然对数的底数)。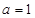 时,求函数
时,求函数 在区间
在区间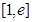 上的最大值和最小值;
上的最大值和最小值; 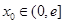 ,在
,在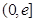 上总存在两个不同的
上总存在两个不同的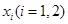 ,使得
,使得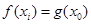 成立,求
成立,求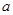 的取值范围。
的取值范围。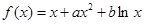 ,曲线
,曲线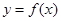 过点
过点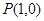 ,且在
,且在 点处的切线斜率为2.
点处的切线斜率为2.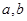 的值;
的值;