Question

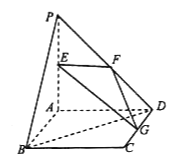
【题目】如图，在四棱锥中，底面为直角梯形，，为等边三角形，，是的中点.

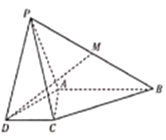
（1）证明：平面平面；

（2）求直线与平面所成角的正弦值.

Answer 1

【答案】（1）证明见解析；（2）

【解析】

（1）要证面面平行即证线面平行，可根据面面平行的判定定理求证，可通过平面来进行求证；

（2）线面角正弦值的求法可通过等体积法进行转化，通过求出点到平面距离，再结合正弦三角函数定义即可求解

（1）取的中点，连结，

∵分别是的中点，

∴，且，

∵，

∴，

∴，∴，

∵，∴平面，

∵平面，∴平面平面.

（2）如图，连结，

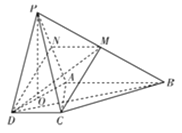
由（1）知平面，∴，

在中，，同理，

在梯形中， ，，

∵，为的中点，∴，

由题意得，

，

设为的中点，连结，由题意得，

∵平面平面，平面，平面平面，

∴平面，

设点到平面的距离为，

∵，∴，解得.

∵，∴直线与平面所成角的正弦值.