题目内容
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=AA1=1,延长A1C1至点P,使C1P=A1C1 , 连接AP交棱CC1于点D. (Ⅰ)求证:PB1∥平面BDA1;
(Ⅱ)求二面角A﹣A1D﹣B的平面角的余弦值.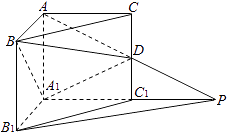
【答案】解:以A1为原点,A1B,A1C,A1A分别为x轴,y轴,z轴正方向,建立坐标系, 则A1(0,0,0),B1(1,0,0),C1(0,1,0),B(1,0,1),P(0,2,0)
(Ⅰ)在△PAA1中,C1D= ![]() AA1,则D(0,1,
AA1,则D(0,1, ![]() )
)
∴ ![]() =(1,0,1),
=(1,0,1), ![]() =(0,1,
=(0,1, ![]() ),
), ![]() =(﹣1,2,0)
=(﹣1,2,0)
设平面BDA1的一个法向量为 ![]() =(a,b,c)
=(a,b,c)
则 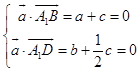
令c=﹣1,则 ![]() =(1,
=(1, ![]() ,﹣1)
,﹣1)
∵ ![]()
![]() =1×(﹣1)+
=1×(﹣1)+ ![]() ×2+(﹣1)×0=0
×2+(﹣1)×0=0
∴PB1∥平面BDA1
(Ⅱ)由(I)知平面BDA1的一个法向量 ![]() =(1,
=(1, ![]() ,﹣1)
,﹣1)
又 ![]() =(1,0,0)为平面AA1D的一个法向量
=(1,0,0)为平面AA1D的一个法向量
∴cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() =
= ![]()
故二面角A﹣A1D﹣B的平面角的余弦值为 ![]()
【解析】以A1为原点,A1B,A1C,A1A分别为x轴,y轴,z轴正方向,建立坐标系,则我们易求出各个点的坐标,进而求出各线的方向向量及各面的法向量.(I)要证明PB1∥平面BDA1 , 我们可以先求出直线PB1的向量,及平面BDA1的法向量,然后判断证明这两个向量互相垂直(II)由图象可得二面角A﹣A1D﹣B是一个锐二面角,我们求出平面AA1D与平面A1DB的法向量,然后求出两个法向量夹角的余弦值,得到结论.
【考点精析】通过灵活运用直线与平面平行的判定和直线与平面平行的性质,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行;简记为:线面平行则线线平行即可以解答此题.

【题目】某公司共有职工1500人,其中男职工1050人,女职工450人.为调查该公司职工每周平均上网的时间,采用分层抽样的方法,收集了300名职工每周平均上网时间的样本数据(单位:小时)

男职工 | 女职工 | 总计 | |
每周平均上网时间不超过4个小时 | |||
每周平均上网时间超过4个小时 | 70 | ||
总计 | 300 |
(Ⅰ)应收集多少名女职工样本数据?
(Ⅱ)根据这300个样本数据,得到职工每周平均上网时间的频率分布直方图(如图所示),其中样本数据分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .试估计该公司职工每周平均上网时间超过4小时的概率是多少?
.试估计该公司职工每周平均上网时间超过4小时的概率是多少?
(Ⅲ)在样本数据中,有70名女职工的每周平均上网时间超过4个小时.请将每周平均上网时间与性别的![]() 列联表补充完整,并判断是否有95%的把握认为“该公司职工的每周平均上网时间与性别有关”
列联表补充完整,并判断是否有95%的把握认为“该公司职工的每周平均上网时间与性别有关”