题目内容
(本小题12分)
已知函数
(1)求函数 的单调区间和极值;
的单调区间和极值;
(2)已知 的图象与函数
的图象与函数 的图象关于直线
的图象关于直线 对称,证明:当
对称,证明:当 时,
时, ;
;
(3)如果 且
且 ,证明:
,证明:
已知函数

(1)求函数
 的单调区间和极值;
的单调区间和极值;(2)已知
 的图象与函数
的图象与函数 的图象关于直线
的图象关于直线 对称,证明:当
对称,证明:当 时,
时, ;
;(3)如果
 且
且 ,证明:
,证明:
(1)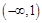 增,
增,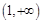 减
减
(2) (3)见解析
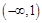 增,
增,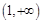 减
减(2) (3)见解析
(1)直接求导利用导数大(小)于零求其单调增(减)区间,再根据极值点左正右负是极大值点,左负右正是极小值点。
(2)先根据图像关于x=1对称,可知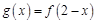 确定出y=g(x)的解析式。然后令
确定出y=g(x)的解析式。然后令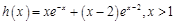 ,再利用导数求h(x)的最小值,证明h(x)min>0即可。
,再利用导数求h(x)的最小值,证明h(x)min>0即可。
(3)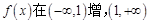 减,且由(2)可知,
减,且由(2)可知, 不可能同时大于1或同时小于1
不可能同时大于1或同时小于1
所以只可能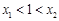 ,
,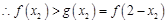 ,又
,又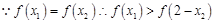
又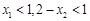 到此问题得以解决。
到此问题得以解决。
解:(1)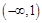 增,
增,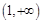 减
减
(2)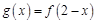
欲证 时,
时,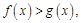 即证
即证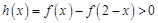
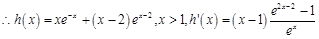
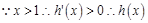 在
在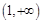 上单调递增
上单调递增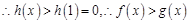 在
在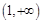 上成立.
上成立.
(3)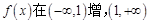 减,且由(2)可知,
减,且由(2)可知, 不可能同时大于1或同时小于1
不可能同时大于1或同时小于1
所以只可能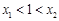 ,
,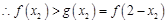
又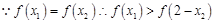
又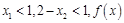 在
在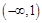 上单调增
上单调增
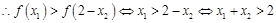
(2)先根据图像关于x=1对称,可知
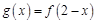 确定出y=g(x)的解析式。然后令
确定出y=g(x)的解析式。然后令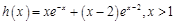 ,再利用导数求h(x)的最小值,证明h(x)min>0即可。
,再利用导数求h(x)的最小值,证明h(x)min>0即可。(3)
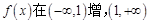 减,且由(2)可知,
减,且由(2)可知, 不可能同时大于1或同时小于1
不可能同时大于1或同时小于1所以只可能
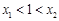 ,
,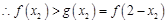 ,又
,又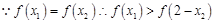
又
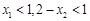 到此问题得以解决。
到此问题得以解决。解:(1)
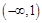 增,
增,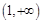 减
减(2)
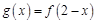
欲证
 时,
时,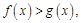 即证
即证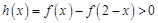
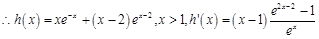
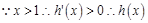 在
在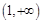 上单调递增
上单调递增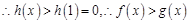 在
在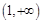 上成立.
上成立.(3)
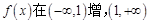 减,且由(2)可知,
减,且由(2)可知, 不可能同时大于1或同时小于1
不可能同时大于1或同时小于1所以只可能
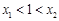 ,
,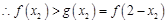
又
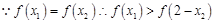
又
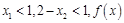 在
在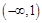 上单调增
上单调增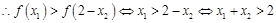

练习册系列答案
相关题目
 ,
,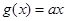 ,
,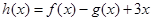 ,其中
,其中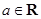 且
且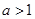 .
.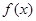 的导函数
的导函数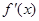 的最小值;
的最小值;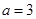 时,求函数
时,求函数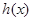 的单调区间及极值;
的单调区间及极值;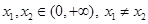 ,函数
,函数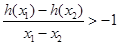 ,求实数
,求实数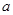 的取值范围.
的取值范围.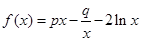 ,且
,且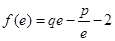 ,其中
,其中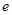 是自然对数的底数.
是自然对数的底数.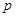 与
与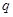 的关系;
的关系;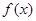 在其定义域内为单调函数,求
在其定义域内为单调函数,求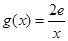 ,若在
,若在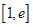 上至少存在一点
上至少存在一点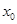 ,使得
,使得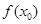 >
> 成立,求实数
成立,求实数
 在
在 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围; 时,求
时,求 上的最大值和最小值;
上的最大值和最小值; ,
, 恒成立.
恒成立. 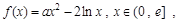 其中
其中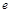 是自然对数的底 .
是自然对数的底 .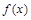 在
在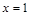 处取得极值,求
处取得极值,求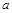 的值;
的值;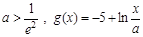 ,存在
,存在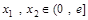 ,使得
,使得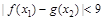 成立,求
成立,求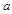 为实数,
为实数,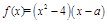 ,
,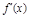 为
为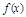 的导函数.
的导函数.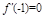 ,求
,求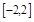 上的最大值和最小值;
上的最大值和最小值;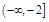 和
和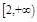 上均单调递增,求
上均单调递增,求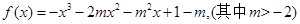 的图像在
的图像在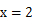 处的切线与直线
处的切线与直线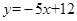 平行。
平行。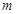 的直线;
的直线;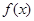 在区间
在区间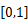 上的最小值;
上的最小值;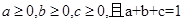 ,利用结论(2)证明:
,利用结论(2)证明: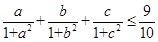
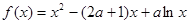
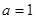 时, 求函数
时, 求函数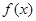 的单调增区间;
的单调增区间;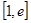 上的最小值;
上的最小值;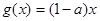 ,若存在
,若存在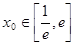 ,使得
,使得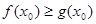 成立,求实数
成立,求实数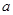 的取值范围.
的取值范围.