题目内容
8.已知在极坐标系下,曲线C:ρ(cosα+2sinα)=4(α为参数)与点A(2,$\frac{π}{3}$).(1)求曲线C与点A的位置关系;
(2)已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标的x轴正半轴重合,直线l:$\left\{\begin{array}{l}{x=1-2t}\\{y=-2+4t}\end{array}\right.$,求曲线C与直线L的交点坐标.
分析 (1)由x=ρcosθ,y=ρsinθ,能求出曲线C的直角坐标方程和点A(2,$\frac{π}{3}$)的直角坐标,由此能判断曲线C与点A的位置关系.
(2)曲线C的直角坐标方程为:x+2y-4=0,直线l:$\left\{\begin{array}{l}{x=1-2t}\\{y=-2+4t}\end{array}\right.$消去参数t,得2x+y=0,联立$\left\{\begin{array}{l}{x+2y-4=0}\\{2x+y=0}\end{array}\right.$,能求出曲线C与直线L的交点坐标.
解答 解:(1)∵在极坐标系下,曲线C:ρ(cosα+2sinα)=4(α为参数),
∴曲线C的直角坐标方程为:x+2y-4=0,
∵在极坐标系下,点A(2,$\frac{π}{3}$),
∴x=$2cos\frac{π}{3}$=1,y=2sin$\frac{π}{3}$=$\sqrt{3}$,
∴A的直角坐标为A(1,$\sqrt{3}$),
∵1+2$\sqrt{3}$-4≠0,∴点A不在曲线C上.
(2)∵曲线C的直角坐标方程为:x+2y-4=0,
直线l:$\left\{\begin{array}{l}{x=1-2t}\\{y=-2+4t}\end{array}\right.$消去参数t,得2x+y=0,
解方程$\left\{\begin{array}{l}{x+2y-4=0}\\{2x+y=0}\end{array}\right.$,得x=-$\frac{4}{3}$,y=$\frac{8}{3}$,
∴曲线C与直线L的交点坐标(-$\frac{4}{3}$,$\frac{8}{3}$).
点评 本题考查曲线与点的位置关系的判断,考查曲线与直线的交点坐标的求法,是基础题,解题时要注意极坐标方程、参数方程和直角坐标方程转化公式的合理运用.

 阅读快车系列答案
阅读快车系列答案| A. | B⊆∁UA | B. | A∩B=∅ | C. | A⊆∁UB | D. | ∁UA∩∁UB=∅ |
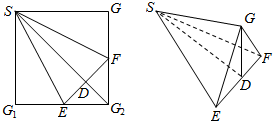 如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3中点,D是EF与SG2的交点,现沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体G-SEF中必有( )
如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3中点,D是EF与SG2的交点,现沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体G-SEF中必有( )| A. | SD⊥平面EFG | B. | SE⊥GF | C. | EF⊥平面SEG | D. | SE⊥SF |
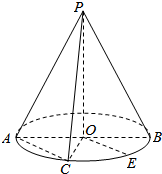 如图,圆锥的顶点为P,底面圆为O,底面的一条直径为AB,C为半圆弧$\widehat{AB}$的中点,E为劣弧$\widehat{CB}$的中点,已知PO=2,OA=1,
如图,圆锥的顶点为P,底面圆为O,底面的一条直径为AB,C为半圆弧$\widehat{AB}$的中点,E为劣弧$\widehat{CB}$的中点,已知PO=2,OA=1, 如图,在直三棱柱ABC-A1B1C1中,AA1=AC=2AB=2,且BC1⊥A1C.
如图,在直三棱柱ABC-A1B1C1中,AA1=AC=2AB=2,且BC1⊥A1C.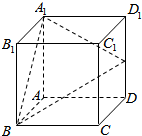 如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.
如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.